An extension to the Fourier and Laplace transforms for sampled-data signals. The Laplace transform G(s) of a sampled-data signal x(t) is given by:

where s is the complex operator σ + jω (see s-domain circuit analysis) and T is the sampling period. A new variable is defined, z = e^sT, and the z transform G(z) of the signal x(t) becomes:

Since z = e^sT and s = σ + jω, then z = e^σT e^jωT. The term e^–jωT implies a constant time delay of T seconds, and for this reason z is often referred to as the shift operator or the z transform operator.

Since z has both real and imaginary parts it can be plotted on the complex plane known as the z-plane in a similar fashion to points on the s-plane (see s-domain circuit analysis). The relationship between the s-plane and the z-plane is shown in the diagram. It can be seen that the left-hand half of the s-plane maps into the area inside the circle, called the unit circle, in the z-plane.

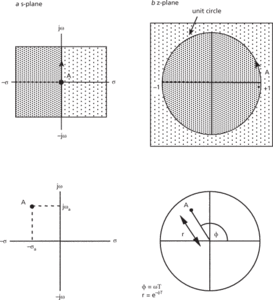
Z transform: relationship between (a) s-plane and (b) z-plane