A method originated by Legendre, which refers to the process of estimating the unknown parameters of a model by minimizing the sum of squared differences between the observed values of a random variable and the values predicted by the model. If every observation is given equal weight then this is ordinary least squares (OLS).

For example, with n pairs of observations (x₁, y₁), …, (x_n, y_n) and the linear regression model

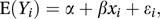
where α and β are unknown parameters, ε_j is an error of observation, and E(Y_j) denotes the expected value of Y_j, the ordinary least squares estimates are the values for α and β that minimize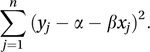See also generalized least squares; weighted least squares.