Let f and g be two real functions on the interval [a,b] and assume that g(x) > 0 for all x.

If m ≤ f(x) ≤ M for all x, then

If f is a continuous function on [a,b], then there exists c in (a,b) such that

Let f be a function that is continuous on [a, b] and differentiable in (a, b). The mean value theorem then states that there is a number c with a  <  c  <  b such that

This can be equivalently expressed as:there is a point C on the graph of f where the tangent is parallel to the line segment joining A(a,f(a)) to B(b,f(b)). If A, with coordinates (a, f(a)), and B, with coordinates (b, f(b)), are the points on the graph corresponding to the end‐points of the interval, there must be a point C on the graph between A and B at which the tangent is parallel to the chord AB.

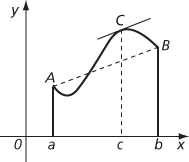
Mean gradient achieved at C

Rolle’s Theorem is a special case of the mean value theorem. Taylor’s Theorem is an extension of the mean value theorem. The mean value theorem has two immediate corollaries:

1. (i) if f′(x) = 0 for all x, then f is a constant function,

2. (ii) if f′(x)  >  0 for all x, then f is strictly increasing.