Abbreviation for analysis of variance, it refers to the attribution of variation in a variable to variations in one or more explanatory variables. The term was introduced by Sir Ronald Fisher in 1918.

A measure of the total variability in a set of data is given by the sum of squared differences of the observations from their overall mean. This is the total sum of squares (TSS). It is often possible to subdivide this quantity into components that are identified with different causes of variation. The full subdivision is usually set out in a table, as suggested by Sir Ronald Fisher in his 1925 book Statistical Methods for Research Workers. Each row of the table is concerned with one or more of the components of the observed variation. The columns of the table usually include the sum of squares (SS), the corresponding number of degrees of freedom (ν), and their ratio, the mean square (=SS/ν).

After the contributions of all the specified sources of variation have been determined, the remainder, often called the residual sum of squares (RSS) or error sum of squares, is attributed to random variation. The mean square corresponding to RSS is often used as the yardstick for assessing the importance of the specified sources of variation. One method involves comparing ratios of mean squares with the critical values of an F-distribution.

As an example, suppose that four varieties of tomatoes are grown in three grow-bags giving the yields (in g) shown below. The explanatory variables are the grow-bags and the varieties.

The following ANOVA table results:

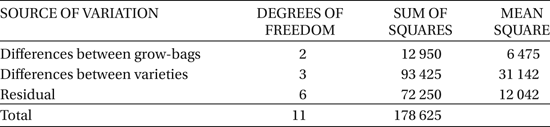
Since the mean square for varieties is much greater than that for grow-bags we can conclude that differences between varieties are more important. However, the residual sum of squares amounts to nearly half the total sum of squares, indicating that there are major unexplained sources of variation.

The proportion of variation explained by the model is R² given by

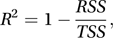
which is sometimes called the squared multiple correlation or the coefficient of determination. In the example R²=0.60. The quantity 1−R² is the coefficient of alienation. In the case of a linear relation between two variables, R² is the square of the sample correlation coefficient.

A quantity often calculated is the adjusted R² in which, in the previous formula, RSS is replaced by RSS/(n−p−1) and TSS is replaced by TSS/(n−1), where n is the number of observations and p is the number of parameters in the model. In the example, n=12, p=5 and the adjusted R² is 0.26.

In 1989, Sir David Cox and E. Joyce Snell introduced a more general definition based on the likelihood. For a sample of size n, let denote the maximum of the likelihood based on some proposed model involving the parameters β, and let L(0) denote the likelihood when all parameters are set to zero. The Cox–Snell R² is

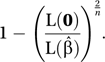
A preferable statistic, in the sense that all values between 0 and 1 can be achieved, is obtained by dividing the Cox–Snell R² by its maximum value . This variation was suggested in 1991 for a discrete model by the Dutch medical statistician Nico J. D. Nagelkerke and is now described as Nagelkerke's R².

The proportion of the total sum of squares that is attributed to any particular source of variation is referred to as eta-squared (η²). Thus, the difference between grow-bags has . A related statistic is partial eta-squared, which is the ratio of the sum of squares of interest to the total of that sum of squares and the residual sum of squares. Thus, for grow-bags, the partial eta-squared is

Often, particular comparisons between the treatments are of interest. These are referred to as contrasts. The set of contrasts consisting of, say, (i) a comparison of treatment 1 with the average effect of treatments 2 to t, (ii) a comparison of treatment 2 with the average effect of treatments 3 to t, etc. are called Helmert contrasts. Both these contrasts and those corresponding to orthogonal polynomials lead to a diagonal variance–covariance matrix.

In an ANOVA analysis each explanatory variable takes one of a small number of values. If, instead, some explanatory variables are continuous in nature (see continuous variable), then the resulting models are called ANOCOVA models (also ANCOVA or analysis of covariance models). ANOVA can also be thought of as multiple regression using only dummy variables. See also experimental design.