A two-player game that has no pure strategy equilibrium but does have a unique mixed strategy equilibrium. The players simultaneously place pennies on a table. Player 1 receives a payment of £1 from player 2 if the faces on the pennies differ (one being heads and the other being tails). Player 2 receives a payment of £1 from player 1 if the faces match. These pay-offs are shown in the pay-off matrix.

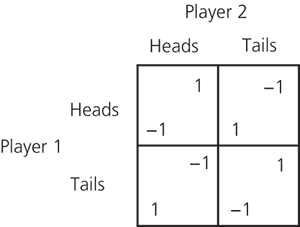
It is easy to see there is no pure strategy equilibrium. Assume there is a pure strategy equilibrium. If the two players choose the same strategy then player 1 will wish to deviate. If the two players choose different strategies then player 2 will wish to deviate. The unique mixed strategy is to play each pure strategy with probability one half.