A two-sample non-parametric test, equivalent to the Wilcoxon rank-sum test, introduced in 1947 by Mann and Whitney. It is assumed that the samples are random and come from populations (random variables X and Y) that have the same distribution after a translation of size k: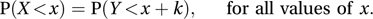The null hypothesis is that the random variables have the same distribution (i.e. k=0). See also test for equality of location.

With samples of sizes m and n (m≤n), the first stage is the replacement of the (m+n) observed values by their ranks in the combined sample. For the (smaller) sample of size m, denote the sum of the ranks by R. The distribution of R is approximately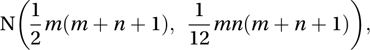so that the test statistic, z, is given by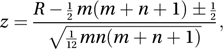where the ±½ is a continuity correction with sign chosen so as to reduce the absolute magnitude of the numerator.

For example, suppose that the marks obtained by a small random sample of statistics students were as follows: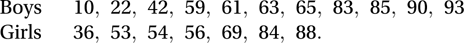The question of interest is whether the data support the null hypothesis of a common mark distribution. The ranks are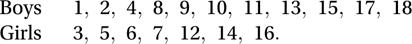Working with the (smaller) set of girls, m is 7 and R is 3+5 +⋯+16=63. Using n=11, the test statistic, z, is given by 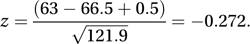Since |z|<1.96, we accept, at the 5% significance level, the hypothesis that the two sets of marks have come from the same distribution.