A measure of the association between a binary variable (see Bernoulli distribution), X, taking values 0 and 1, and a continuous random variable, Y. If it is assumed that for each value of X the distribution of Y is a normal distribution, with different means but the same variance, then an appropriate measure is the point biserial correlation coefficient. This is estimated from a sample as r_pb (−1≤r_pb≤1), given by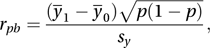where y¯₁ and y¯₀ are the mean Y-values corresponding to the two values of X, is the sample variance (using the n−1 divisor) of the combined set of n Y-values, and p is the proportion of X values equal to 1.

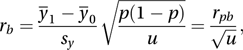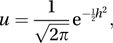If it can be assumed that X is a dichotomous (See categorical variable) representation of an underlying continuous random variable, W, with W and Y having a bivariate normal distribution (see multivariate normal distribution), then an appropriate measure is the biserial correlation coefficient. This is estimated as r_b, given bywhereand h is the value defined by P(Z≥h)=p, for a standard normal variable (see normal distribution) Z.