An isometry of ℝⁿ of the form p ↦ p′‎ = p + h, where h is constant. So, in the plane, point P with coordinates (x,y) is mapped to the point P′ with coordinates (x′, y′), where x′=x + h₁, y′=y + h₂. Thus the origin O is mapped to the point O′ with coordinates (h₁, h₂), and the point P is mapped to the point P′, where the directed line segment $\overrightarrow{PP\prime }$ has the same direction and length as $\overrightarrow{OO\prime }.$

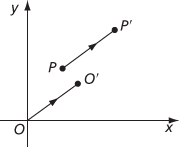
Effect of a translation on O and P

See Euclidean group.