ANOVA with a multivariate distribution for the response variable. With g groups and n_j observations in the jth group, the three basic matrix quantities involve various sums of squares and cross-products. As with ANOVA the idea is to divide the total variation into a contribution explained by differences between the groups and a residual contribution resulting from variation within groups. 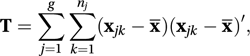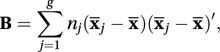The corresponding matrices are T, B, and W, defined by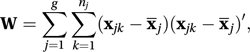where x̄_j is the column vector of means for the jth group, and x̄ is the column vector of overall means.

The most usual test of the hypothesis that the groups come from a single population uses Wilks's lambda (Λ), given by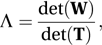where det(M) denotes the determinant of the matrix M. Alternative tests use the Hotelling–Lawley trace (the sum of the eigenvalues of BW⁻¹), the Pillai–Bartlett trace (the sum of the eigenvalues of BT⁻¹), and Roy’s maximum root (the largest eigenvalue of BW⁻¹).