A line that a curve approaches but only touches at infinity.
A line l is an asymptote to a curve if the distance from a point P to the line l tends to zero as P tends to infinity along some unbounded part of the curve. Consider the following examples:
Example (i) has x =−2 and x =1 as vertical asymptotes and y = 0 as a horizontal asymptote. Example (ii) has no vertical asymptotes and y = 3 as a horizontal asymptote. To investigate example (iii), it can be rewritten as
Then it can be seen that y = x−1 is a slant (or oblique) asymptote, that is, an asymptote that is neither vertical nor horizontal.
If part of a graph is unbounded and there is a fixed straight line l such that the distance from a point P on the graph to l tends to 0 as OP → ∞, where O is the origin, then l is an asymptote to the curve. Alternatively, it is the limiting position of the tangent to the graph at P, as OP → ∞. For example, the asymptotes of the graph of
 are y=2x+3 and x=2.
are y=2x+3 and x=2.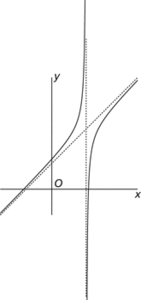
Asymptote. The dotted lines are the asymptotes (vertical, x=2; oblique, y=2x+3) of the graph y=2x+3−.
A straight line that is closely approached by a curve so that the perpendicular distance between them decreases to zero at an infinite distance from the origin.
- hydrology
- Hydrology and Water Resources Programme
- hydrolysate
- hydrolysis
- hydromagnesite
- hydrometallurgy
- hydrometeor
- hydrometer
- hydromorphic
- hydromorphology
- hydromuscovite
- hydron
- hydronium ion
- hydrophilic
- hydrophily
- hydrophobic
- hydrophone
- hydrophyte
- hydroponics
- hydroprocessing
- hydropyrolysis
- hydroquinone
- hydrorefining
- hydrosere
- hydroskimming