An experimental design related to Latin square and balanced incomplete block designs. As an example, suppose there are nine treatments A–I. The design consists of two squares:
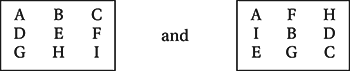
Considering the squares separately, we find that each pair of treatments occurs exactly once—either in a row or in a column. In general, with n2 treatments, the design requires (n−1) separate n×n squares.
- backward-bending supply curve
- backward causation
- backward chaining
- backward compatibility
- backward difference
- backward diode
- backward elimination
- backward error analysis
- backward error correction
- backward error recovery
- backward induction
- backward integration
- backward scan
- backward substitution
- backward-wave oscillator
- backwash
- backwashing
- Bacon, Francis (1561–1626)
- Bacon, Francis, 1st Baron Verulam, Viscount St Albans (1561–1626)
- Baconian method
- Bacon, Roger (c.1214–92)
- Bacon’s Rebellion (1676)
- Bacteria
- bacteria
- bacterial artificial chromosome