A general test, published in 1952, that compares the fit of the observed cumulative distribution function with that expected. It was derived by Anderson and David A. Darling as a modification of the Cramér–von Mises test. The test statistic A2 is given by
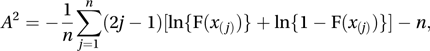where F is the hypothesized cumulative distribution function, n is the sample size, and x(j) is the jth ordered observation (x(1)≤x(2)≤⋯≤x(n)). The statistic can also be used to test for normal distribution and exponential distribution with unknown parameters estimated by their sample equivalents. In some cases, as shown in the following table, an adjusted test statistic is required.test statistic
upper tail probability
0.10
0.05
0.025
0.01
Specified distribution
A2
1.933
2.492
3.070
3.857
Normal, estimated mean (n>20)
A2
0.894
1.087
1.285
1.551
Normal, estimated variance (n>20)
A2
1.743
2.308
2.898
3.702
Normal, estimated mean and variance
0.631
0.752
0.873
1.035
Exponential, estimated mean
1.062
1.321
1.591
1.959
- overfitting
- overflow
- overflow channel
- overflowing well
- overflow levée
- overfold
- overfull employment
- overhead costs
- overhead product
- overheating
- overland flow
- overlap
- cyclic phosphorylation
- cyclic polygon
- cyclic redundancy check
- cyclic redundancy checks
- cyclic sedimentation
- cyclic system
- cyclic vector
- cyclic voltammetry
- cyclin
- cycling
- cycling pool
- cyclization
- cyclo-