Given vectors a and b, let $\overrightarrow{OA}$ and $\overrightarrow{OB}$ be directed line segments that represent a and b, with the same initial point O. The sum of $\overrightarrow{OA}$ and $\overrightarrow{OB}$ is the directed line segment $\overrightarrow{OC}$, where $OACB$ is a parallelogram, and the sum a + b is defined to be the vector c represented by $\overrightarrow{OC}$. Alternatively, the sum of vectors a and b can be defined by representing a by a directed line segment $\overrightarrow{OP}$ and b by $\overrightarrow{PQ}$ where the final point of the first directed line segment is the initial point of the second. Then a + b is the vector represented by $\overrightarrow{OQ}$. Addition of vectors has the following properties, which hold for all a, b, and c:

1. (i) a + b = b + a, the commutative law.

2. (ii) a + (b + c)=(a + b) + c, the associative law.

3. (iii) a + 0 = 0 + a = a, where 0 is the zero vector.

4. (iv) a + (−a)=(−a) + a = 0, where −a is the negative of a.

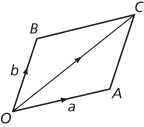
Parallelogram law for addition

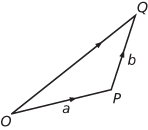
Triangle law for addition

Addition of coordinate vectors in n-dimensional space is done componentwise. So if a = (a₁, a₂,…,a_n) and b = (b₁, b₂,…,b_n), then a + b = (a₁ + b₁, a₂ + b₂,…, a_n + b_n).