Events A and B are independent if the occurrence of either does not affect the probability of the other occurring. Otherwise, A and B are dependent. For independent events, the probability that they both occur is given by the product law Pr(A ∩ B) = Pr(A) Pr(B). This is equivalent to the conditional probability Pr(A | B) equalling Pr(A), provided Pr(B)≠0.
For example, when an unbiased coin is tossed twice, the probability of obtaining ‘heads’ on the first toss is , and the probability of obtaining ‘heads’ on the second toss is . These two events are independent. So the probability of obtaining ‘heads’ on both tosses is equal to .
Two events (see sample space) A and B are independent events if
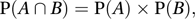
or, equivalently, if P(A|B) = P(A), or if P(B|A) = P(B). Three events A, B, and C are said to be independent (or mutually independent) if each pair is independent and if, in addition,
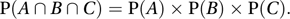 For a set of more than three events to be independent the multiplication law for probabilities must hold for all possible subsets. See also conditional probability; intersection; pairwise independent.
For a set of more than three events to be independent the multiplication law for probabilities must hold for all possible subsets. See also conditional probability; intersection; pairwise independent.
- annotations((in bioinformatics))
- announcement effect
- announcement newsgroup
- announcement of opportunity
- annoyance bot
- annual
- annual aberration
- annual equation
- annual general meeting
- annual inequality
- annualized growth rate
- annualized percentage rate of interest
- annual parallax
- Annual Population Survey
- annual report and accounts
- annual rhythm
- annual ring
- annual snow-line
- annual variation
- annuity
- annuity factor
- annuity rate
- annular drainage
- annular eclipse
- annular flow