The distribution of the number of independent Bernoulli trials before a successful result is obtained; for example, the distribution of the number of times a coin has to be tossed before a head comes up. The probability that the number of trials (x) is k is
The mean and variance are 1/p and q/p2 respectively.
The discrete probability distribution for the number of experiments required to achieve the first success in a sequence of independent experiments, all with the same probability p of success. The probability mass function is given by Pr(X = r) = p(1−p)r−1, for r = 1, 2,…. It has mean 1/p and variance (1−p)/p2.
A particular discrete distribution. An experiment or trial with two possible results, usually classified as ‘success’ or ‘failure’, is repeated independently until the first success is obtained. If the probability of a success, p (≠ 0, 1), is the same for each trial, then the distribution of the total number of trials, up to and including the one in which the first success is obtained, is a geometric distribution with parameter p. The probability function is given by
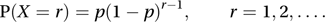
The reason for the term ‘geometric’ is that the sequence of probabilities P(X = r), for r = 0, 1, 2,…, forms a geometric progression with first term p and common ratio (1−p). The mean is 1/p and the variance is (1−p)/p2. The mode is 1 for all values of p.
The fact that the mode is always 1 means that, even for a very rare event (e.g. a lottery win), the most probable number of trials necessary to obtain the first success is 1. This is sometimes regarded as a paradox.
If we write q = 1−p, cumulative probabilities are given by P(X≥r) = qr−1 and P(X≤r) = 1−qr. The geometric distribution is a discrete analogue of the exponential distribution and shares the ‘non-ageing’ or forgetfulness property:
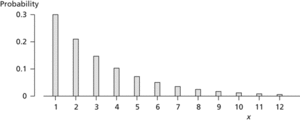
Geometric distribution. All geometric distributions have their mode at the lowest possible value, with successive probabilities having the common ratio p.
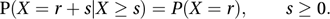
If X1, X2,…, Xn are independent random variables each having a geometric distribution with parameter p, then , which is the number of trials up to and including the nth success, has a negative binomial distribution with parameters n and p.
Some authors take the definition of a geometric distribution to be the number of trials before the first successful trial. This leads to P(X=r)=p(1−p)r, for r=0, 1,…, for which the mean is (1−p)/p and the mode is 0, though the variance is unchanged.
See log-normal.
A discrete distribution with a probability function of the form
for x = 1,2,…and 0 ≤ p ≤ 1. The geometric distribution has mean 1/p and variance (1− p)/p2.
- phenoclast
- phenocopy
- phenocryst
- phenogram
- phenol
- phenolic resins
- phenology
- phenolphthalein
- phenolphthalein test
- phenols
- phenol–formaldehyde resin
- phenome
- phenomena bene fundata
- phenomenalism
- phenomenological relations
- phenomenology
- phenomenon
- phenomenon instance
- phenon
- phenotype
- phenotypic plasticity
- phenoxy resins
- phenylalanine
- phenylamine
- phenylammonium ion