A wave-like oscillation in which an amplitude starts at zero, goes to a maximum, and then returns to zero. There are many physical examples of wavelets, including some that can be detected in a seismograph. Wavelets can also be used in signal processing.
Functions that provide succinct and accurate representations of time series and arrays of spatial data. Wavelets have great potential as tools for data compression, when the data consist of, for example, images to be sent across computer networks. The wavelet representation of g(t), a continuous function of time t, has the form
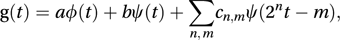 where n and m are integers, with n≥1 and m≥0. The function ψ is the mother wavelet and φ is the scaling function or father wavelet. This wavelet representation of g(t) has similarities to a Fourier series representation but is more flexible, since both φ and ψ are chosen to take the value 0 outside finite intervals. For a time series measured at N equi-spaced time points, the functions φ and ψ are related by the equations
where n and m are integers, with n≥1 and m≥0. The function ψ is the mother wavelet and φ is the scaling function or father wavelet. This wavelet representation of g(t) has similarities to a Fourier series representation but is more flexible, since both φ and ψ are chosen to take the value 0 outside finite intervals. For a time series measured at N equi-spaced time points, the functions φ and ψ are related by the equations 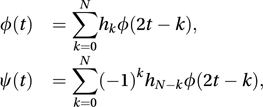 where h0, h1,…, hN are constants, referred to as filter coefficients. The original N data values are represented by a sum of a weighted combination of the father and mother wavelets together with daughter wavelets. The daughter wavelet, ψjk, is related to the mother wavelet, ψ, by a simple formula that reflects a translation and dilation of the mother, so that the daughter looks like a compressed version of its mother. The relation is
where h0, h1,…, hN are constants, referred to as filter coefficients. The original N data values are represented by a sum of a weighted combination of the father and mother wavelets together with daughter wavelets. The daughter wavelet, ψjk, is related to the mother wavelet, ψ, by a simple formula that reflects a translation and dilation of the mother, so that the daughter looks like a compressed version of its mother. The relation is 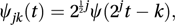 where 0≤t < 1. The coefficient simplifies subsequent analysis.
where 0≤t < 1. The coefficient simplifies subsequent analysis.A summary of the wavelet decomposition for the case N=16 is illustrated in the table:

Each of the ψ functions is a piecewise continuous function that takes the value 0 outside its range of influence. Thus, if observation 14 takes an unusually large value then this will be reflected in an unusually large coefficient of ψ36; if observations 5 to 8 are unusually small then this will be reflected in an unusually small coefficient of ψ21; and so on.
The first mother wavelet was given in the appendix of the 1909 PhD thesis by Haar. This Haar wavelet is given by
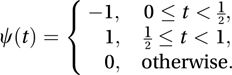 The family of wavelets that are currently most used were introduced by Daubechies in 1988. These wavelets have fractal properties. Other families of wavelets include symmlets and coiflets.
The family of wavelets that are currently most used were introduced by Daubechies in 1988. These wavelets have fractal properties. Other families of wavelets include symmlets and coiflets.
Mother wavelets. The D2 wavelet is the Haar wavelet. The wavelets illustrated here are the D4, D12, and D20 wavelets. All are members of the Daubechies family.
A basis function, W, that yields the representation of a function f(x) of the form:
Wavelets are based on two fundamental ideas: dilation and translation. The construction of wavelets begins with the solution to a dilation equation:ϕ(x) is called the scaling function. W can then be derived from ϕ(x):Wavelets are particularly useful for representing functions that are local in time and frequency. The idea of wavelets grew out of seismic analysis and is now a rapidly developing area in mathematics. There are elegant recursive algorithms for decomposing a signal into its wavelet coefficients and for reconstructing a signal from its wavelet coefficients.
- economizer
- economy
- econophysics
- ecophenotype
- ecophenotypic effects
- ecophenotypy
- ecoregion
- E corona
- ecosphere
- ecostratigraphy
- ECOSTRESS
- ecosystem
- ecosystem services
- ECOSystem Spaceborne Thermal Radiometer Experiment on Space Station
- ecotaxation
- ecotone
- ecotope
- ecotourism
- ecotoxicology
- ecotype
- Eco, Umberto (1932–2016)
- ecozone
- ECQ
- ecruiting
- ECS