Distribution that describes the variation in the values of a statistic over all possible samples. For example, if n values are sampled from a population and if X₁, X₂,…, X_n, are the random variables representing the individual sample values, then X̄, given by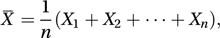is a random variable. The variability of the n values about their mean,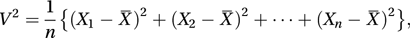is also a random variable. The form of the sampling distributions of X̄ and V² will depend on the population, but statements can nevertheless be made about their moments. If the population has mean μ and variance σ², then, for an infinite population, or for sampling with replacement from a finite population, each of X₁, X₂,…has mean μ and variance σ². Consequently the expected value of X̄ is μ and the expected value of V² is . This shows that X̄ and are unbiased estimators of μ and σ², respectively. The variance of the sample mean X̄ is .

The sample variance is usually taken to be the value of S², though the value of V² is sometimes used.