Consider two triangles ABC and A′B′C′ lying in the (projective) plane.

The theorem states that if the lines AA′, BB′, and CC′ are concurrent at O, then BC and B′C′ intersect at a point L, CA and C′A′ intersect at M, and AB and A′B′ intersect at N, where L, M, and N are collinear.

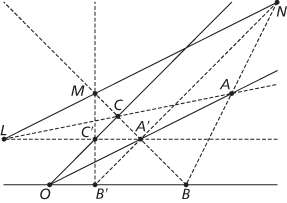
The centre and axis of a perspectivity

O is called the centre of perspectivity of the triangles ABC and A′B′C′ and the line LMN is called the axis of perspectivity. The dual of Desargues’s Theorem is then its converse.