The set of all possible outcomes of an experiment. For example, suppose that an experiment involves tossing a coin three times. Then the sample space could be expressed as
where, for example, ‘HTT’ indicates the tosses came up ‘heads, tails, tails’. See probability space, random variable.
A complete set of all possible results or outcomes for an experiment or observational procedure. The concept was introduced by von Mises in 1931. The sample space is usually denoted by S or E.
An event is a particular collection of outcomes, and is a subset of the sample space. For example, when a die is thrown and the score observed, the sample space is {1, 2, 3, 4, 5, 6}, and a possible event is ‘the score is even’ i.e. {2, 4, 6}. If all the possible outcomes are equally likely, then the probability of an event A is given by
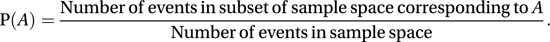The word ‘event’ was used in this context by de Moivre in 1718.The subset of the sample space for the event ‘the score is both even and odd’ is an example of the empty set, usually denoted by ϕ, and P(ϕ)=0.
The subset of the sample space for the event ‘the score is less than 10’, is the whole sample space, S, and P(S)=1.
See also Boolean algebra; complementary event; intersection; union.
- fluxmeter
- fluxoturbidite
- flux quantum
- flux tube
- flux unit
- fly
- flyaround
- flyback
- fly-by
- fly by wire
- fly-by-wire
- flycatcher
- flyer
- flying arrow paradox
- flying fish
- flying fox
- flying geese theory
- Flying Laptop
- flying-spot scanner
- flying squirrel
- Flynn’s classification
- flysch
- flyspeck 3
- flytrap
- flywheel effect