See Pascal’s distribution.
The generalization of the geometric distribution to the waiting time for the kth success in a sequence of independent experiments, all with the same probabilities of success. The probability mass function is given by
This is because the kth success will be on the rth trial if the rth trial is a success and there are k–1 successful trials in the previous r–1 trials. See appendix 15.
For trials classified as ‘success’ or ‘failure’, the distribution of X, the number of trials required in order to obtain n successes. The trials are presumed to be independent and it is assumed that each trial has the same probability of success, p (≠ 0 or 1). The probability function is
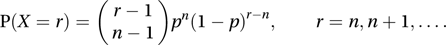 The mean of this distribution is n/p and the variance is n(1−p)/p2.
The mean of this distribution is n/p and the variance is n(1−p)/p2.Special cases of the distribution were discussed by Pascal in 1679. The name ‘negative binomial’ arises because the probabilities are successive terms in the binomial expansion of (P−Q)−n, where P=1/p and Q=(1− p)/p. Writing Y=X−n, an equivalent form for the distribution is
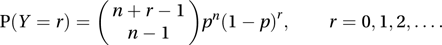 The variable X may be regarded as the sum of n independent geometric variables, each with parameter p. The case n=1 therefore corresponds to the geometric distribution.
The variable X may be regarded as the sum of n independent geometric variables, each with parameter p. The case n=1 therefore corresponds to the geometric distribution.The arc-sinh transformation, suggested by Anscombe in 1948,
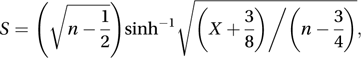 results in a random variable S having an approximate standard normal distribution.
results in a random variable S having an approximate standard normal distribution.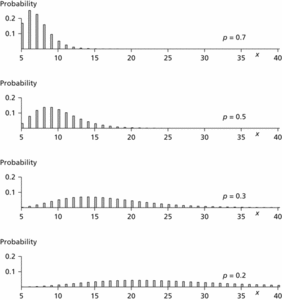
Negative binomial distribution. In each case n=5; the shape is dependent upon the value of p.
- cateniform
- catenin
- catenoid
- Cathar
- catharsis
- cathepsins
- Catherine I (1684–1727)
- Catherine II (1729–96)
- Catherine of Aragon (1485–1536)
- Catherine of Braganza (1638–1705)
- cathetometer
- cathine
- cathinone
- cathode
- cathode dark space
- cathode follower
- cathode glow
- cathode-ray oscilloscope
- cathode rays
- cathode-ray tube
- cathodic protection
- cathodoluminescence
- Catholic emancipation
- Catholicism
- Catholic League