Elementary conductivity theory is an extension of free-electron theory, in which the electrons in a metal are treated as a gas of negatively charged free particles. In a metallic crystal, the average kinetic energy of electrons is very large compared to the energy associated with thermal vibrations in the lattice. Therefore the thermal vibrations have little or no effect on the Fermi level, which represents the maximum energy that these electrons can have. The possible energy states that the electrons can occupy are derived from a particle-in-a-box analysis of the metal crystal.

In the absence of an electric field, the electrons are distributed amongst the possible energy states, up to a maximum energy E_max (or e_F, the Fermi level). Each of these energy states corresponds to a free electron state of motion at a particular speed and direction.

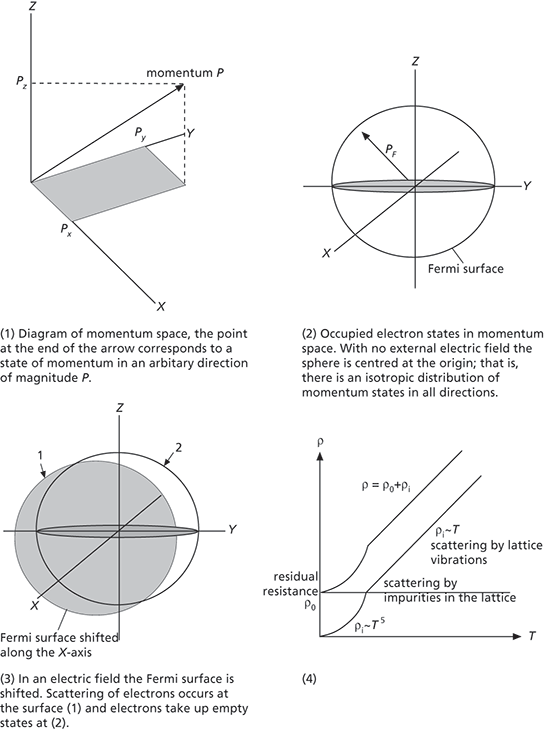
In an electric field, each electron will experience a force that will accelerate it in the direction of the field. A convenient way of illustrating the electric field is to use momentum space diagrams. Each electron state in the particle-in-the-box problem corresponds to a certain momentum possessed by an electron. Imagine a three-dimensional space equipped with a Cartesian coordinate system corresponding to momentum values rather than spatial positions. Each point in this space represents a state of momentum. See diagram (1).

The energy associated with free electrons is restricted to their kinetic energy; therefore the Fermi surface may be represented by the surface of a sphere in the momentum coordinate system, the maximum magnitude of momentum (corresponding to the maximum kinetic energy) being the radius of this sphere. The momentum space diagram for zero field is therefore a sphere centred at the origin, with a radius P_F, which is the magnitude of the maximum momentum at the Fermi surface. See diagram (2). In an electric field applied in the x-direction, the Fermi surface would be shifted in the direction of the field. However, one might expect that maintaining the field would progressively shift the Fermi surface further along the x-direction, as electrons would be accelerated. This does not happen; after a short time a constant current is established whose value depends on the field. The Fermi surface is shifted on application of the field, but only by an amount proportional to the size of the field. See diagram (3).

This stabilization of the current occurs because electrons in states near the Fermi surface are scattered by two main mechanisms: (1) the thermal vibration of the lattice; and (2) the presence of impurity atoms and other point defects. The scattered electrons have their momentum changed by the scattering event and take up states on the other side of the Fermi sphere.

A dynamic equilibrium is therefore established between the electrons being accelerated to the right-hand side of the sphere and those scattered back to the left. On average, the electrons travel the mean free path (λ‎) between each scattering event. The velocity v_F at the Fermi surface is very high, ~10⁶ m/s, compared with any change in velocity produced by the applied field. Therefore, the time between collisions may be considered constant at λ‎/ν‎_F. This means that the shift in the Fermi surface will be greater for a stronger field; i.e. a greater change in velocity can be achieved for a larger field in the same time λ‎/ν‎_F. The current will therefore be higher, which is the basis of Ohm’s law.

Kinetic theory, neglecting scattering by imperfections and lattice vibrations, leads to an estimate of the mean free path. For copper at room temperature this expression gives a value for λ‎ ~ 3.0×10⁻⁸ m. This suggests that electrons in copper can travel up to 100 atomic spacings between collisions. This value of λ‎ is quite surprising as one might expect that a perfect lattice would itself scatter the electrons. However, if the lattice is regular, an electron is attracted to the ions as much in one direction as any other. It is only if the lattice is not perfect that the electrons will be scattered.

As lattice vibrations fall with thermodynamic temperature (T), one would expect that their contribution to resistivity (ρ‎_i) would decrease at low temperatures, eventually becoming zero at 0 K. A more detailed calculation shows that at low temperatures ρ‎_i ∝ T⁵ and changes to a linear dependence on T at higher temperatures. See diagram (4). The theory of electrical conductivity in metals was worked out quantitatively using the quantum theory of solids in the late 1920s and early 1930s. See also band theory.