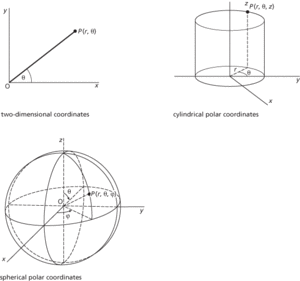
A system used in analytical geometry to locate a point P, with reference to two or three axes. The distance of P from the origin is r, and the angle between the x-axis and the radius vector OP is θ, thus in two-dimensional polar coordinates the coordinates of P are (r,θ). If the Cartesian coordinates of P are (x,y) then x=rcosθ and y=rsinθ.
In three dimensions the point P may be regarded as lying on the surface of a cylinder, giving cylindrical polar coordinates, or on the surface of a sphere, giving spherical polar coordinates. In the former the coordinates of P would be (r,θ,z); in the latter they would be (r,θ,ϕ).
Polar coordinates.
Suppose that a point O in the plane is chosen as origin, and let Ox be a directed line through O, with a given unit of length. For any point P in the plane, let r = |OP| and, if P is not O, let θ be the angle (in radians) that OP makes with Ox, the angle being given a positive sense anticlockwise from Ox. The angle θ satisfies 0 ≤ θ < 2π. Then (r,θ) are the polar coordinates of P.
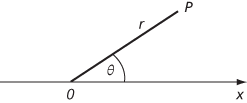
The polar coordinates of P
Suppose that Cartesian coordinates are taken with the same origin and the same unit of length, with positive x-axis along the directed line Ox. Then the Cartesian coordinates (x,y) of a point P can be found from (r,θ), by x = rcosθ, y = rsinθ. Conversely, the polar coordinates can be found from the Cartesian coordinates by , and θ is such that
(Note that θ = tan−1(y/x) but this is not, of itself, sufficient to uniquely determine θ.) In certain circumstances, authors may allow r to be negative, in which case the polar coordinates (r,θ) give the same point as (–r,θ + π).
In mechanics, it is useful, when a point P has polar coordinates (r,θ), to define unit vectors er and eθ by
where i and j are unit vectors in the directions of the positive x- and y-axes. Then er is a unit vector along OP in the direction of increasing r, and eθ is a unit vector perpendicular to this in the direction of increasing θ. These vectors satisfy er∙eθ =0 and er×eθ =k, where k = i×j. See radial and transverse components.
A coordinate system in a plane in which the position of a point P is specified by the distance r=OP, where O is a fixed point (the pole), and the angle θ between OP and a fixed line through O (the initial line). The polar coordinates are given as (r, θ), where r≥0, and −180°<θ≤180° or 0°≤θ<360°. Referred to Cartesian coordinates Oxy, with Ox along the initial line, Cartesian and polar coordinates are related by
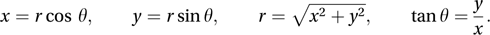
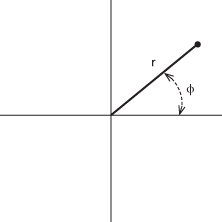
A technique for giving two-dimensional coordinates (r,ϕ) of a point. Radial distance r is the distance along the horizontal x-axis, and polar angle ϕ describes an anti-clockwise rotation. See also cylindrical polar coordinates; spherical polar coordinates.
Polar coordinates
- Venus snow
- VENµS
- veranillo
- verano
- verbal definition
- Vercingetorix (46)
- verdigris
- Verdun, Treaty of (843)
- Vereeniging, Treaty of (31 May 1902)
- Vereiskian
- vergence
- veridical
- verification
- verification and validation
- verification condition
- verification(of a simulation model)
- verification principle
- verification system
- verisimilitude
- VERITAS
- vermiculite
- vermiform appendix
- vernal equinox
- vernalization
- Verneuil process