Given a point P and a non-degenerate conic C, a line L can be associated with P as follows. Two tangent lines to C pass through P, and the points of tangency define the line L. This line is known as the polar of P, and P is known as the pole of L.
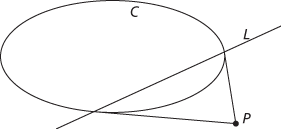
A pole P and polar L
In a projective plane (see projective space), this process gives a one-to-one correspondence between points and lines. If the conic has equation xTBx = 0, where B is a 3×3 symmetric invertible matrix, and P has coordinate vector p, then the equation of the polar is xTBp = 0.
See am herculis star; intermediate polar.
Denoting a component, such as an electrolytic capacitor, that can only operate normally in one direction of applied voltage.
Applying to those parts of the Earth close to the poles. The polar area, in particular the Arctic, is considered to be the forerunner of climate change (Schiermeier (2006) Nature 441, 146). Polar air masses (P) originate in the mid-latitudes (40°–60°) and are characteristically cold.
- dangling else
- dangling reference
- Danian
- Daniel K. Inouye Solar Telescope
- Daniell cell
- Daniell, John Frederic
- Daniell weights
- Daniell window
- Danish Society for Theoretical Statistics
- Danjon scale
- Dansgaard, Willi
- Dansgaard–Oeschger (D–O) cycles
- Dansgaard–Oeschger event
- DANTE
- Dante Alighieri (1265–1321)
- Danto, Arthur C. (1924–2013)
- Danton, Georges (1759–94)
- Dantzig, George Bernard (1914–2005)
- dao
- Daphnia
- DAR
- daraf(symbol: F–1)
- Darboux’s theorem
- Darboux’s theorem(Darboux integral)
- darcy