A probability distribution for a discrete random variable. It is defined, for a variable (r) that can take values in the range 0, 1, 2,…, and has a mean value μ, as
A binomial distribution with a small frequency of success p in a large number n of trials can be approximated by a Poisson distribution with mean np. It is named after the French mathematician and mathematical physicist Siméon-Denis Poisson (1781–1840).
The discrete probability distribution with probability mass function given by
where λ is a positive parameter. The mean and variance both equal λ. The Poisson distribution gives the number of occurrences in a certain time period of an event which occurs randomly but at a constant average rate. It can be used as an approximation to the binomial distribution, where n is large and p is small, by taking λ = np.
A random variable X, whose set of possible values consists of the non-negative integers, with probability function given by
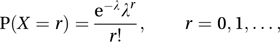 where λ is a positive constant, is said to have a Poisson distribution, or to be a Poisson variable, with parameter λ. (By convention, λ0=1 and 0!=1.) The distribution was named after Poisson, though the first derivation was by de Moivre in 1711. If we note that P(X=0)=e−λ, successive probabilities can be calculated by using the recurrence relation
where λ is a positive constant, is said to have a Poisson distribution, or to be a Poisson variable, with parameter λ. (By convention, λ0=1 and 0!=1.) The distribution was named after Poisson, though the first derivation was by de Moivre in 1711. If we note that P(X=0)=e−λ, successive probabilities can be calculated by using the recurrence relation 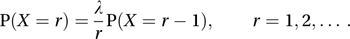 The mean and variance of the distribution are both λ. If λ is not an integer the mode is the value of the integer r for which r−1<λ<r. If λ is an integer then P(X=λ−1)=P(X=λ) and both (λ−1) and λ are modes. If λ<1 the graph of the probability function decreases steadily, whereas if λ>1 the graph increases steadily to the value at the mode, then decreases steadily, tending to 0 as r → ∞.
The mean and variance of the distribution are both λ. If λ is not an integer the mode is the value of the integer r for which r−1<λ<r. If λ is an integer then P(X=λ−1)=P(X=λ) and both (λ−1) and λ are modes. If λ<1 the graph of the probability function decreases steadily, whereas if λ>1 the graph increases steadily to the value at the mode, then decreases steadily, tending to 0 as r → ∞.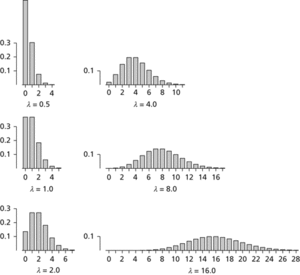
Poisson distribution. The outline of a Poisson distribution with parameter λ increasingly resembles that of a normal distribution as λ increases. Both the mean and the variance of a Poisson distribution with parameter λ are equal to λ.
For large values of λ a normal approximation to the Poisson distribution may be used:
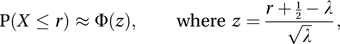 and Φ is the cumulative distribution function for a standard normal variable (see normal distribution). The ‘½’ is a continuity correction. The approximation may be described as ‘For large values of λ a Poisson variable with mean λ is approximately N(λ, λ)’.
and Φ is the cumulative distribution function for a standard normal variable (see normal distribution). The ‘½’ is a continuity correction. The approximation may be described as ‘For large values of λ a Poisson variable with mean λ is approximately N(λ, λ)’.In a Poisson process the number of events in a given region, or a given time interval, has a Poisson distribution.
The basic discrete probability distribution for data in the form of counts of random events. If each event occurs with the same probability and the mean frequency of events is μ, the probability that exactly r events will occur is
The Poisson distribution is discrete, taking the values r=0, 1, 2,… and it can be obtained as a limiting case of the binomial distribution as n tends to infinity while np is held fixed. The mean and variance of the Poisson distribution are both equal to μ.
In statistics, a discrete probability distribution which is applied to the number of times an event occurs.
- confidence ellipse
- confidence interval
- confidence level
- confidence limit
- confidence region
- confidential email system
- confidentiality
- confidentiality(of data)
- configuration
- Configuration Control Board
- configuration file
- configurationism
- configuration management
- configuration space
- configurator
- configured-in, -off, -out
- confined aquifer
- confined space
- confinement
- confining pressure
- confirmation, paradoxes of
- confirmation theory
- confirm(of a statistical experiment)
- conflagration
- confluence