A technique used in geometry to investigate the curvature of surfaces and spaces. A simple and widely used example is to consider a pencil lying on the north pole of a globe and pointing along a meridian. The pencil is moved down this meridian to the equator, and then moved along the equator to some point, while always remaining perpendicular to the equator. The pencil is then moved up the meridian through that point on the equator it has reached until it has been returned to the north pole. The net effect of this parallel transport is that the direction of the pencil has changed although it was not rotated at any time.

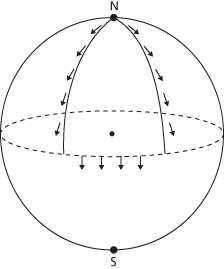
Parallel transport. Consider a traveller who starts at the North Pole, goes to the Equator, goes east for some distance, and then returns to the North Pole, carrying an arrow pointing due south for the entire journey. The direction of the arrow will have changed by some angle when the traveller arrives back at the Pole.

In general, curvature is associated with the failure of certain variables to return to their original values after parallel transport has been performed. Parallel transport has been extensively used in physics to investigate geometrical issues in gauge theories, the general theory of relativity, and quantum mechanics.