【聚合物的流变行为】
拼译：the rheological behaviors of polymer
1851年，史托斯(Stokes)等建立了牛顿流体行为的概念和理论，对于复杂体系的流变行为的实验研究可追溯到1867年麦克斯韦(Maxwell)证实了在各种固体中应力松驰和粘弹行为，1888年，切韦道夫(Schwedoff)测量了在明胶溶液中的蠕变现象，第1次定量地测定了一个接近液体体系的粘弹行为。从20世纪开始，对胶体体系性质的研究作了大量的工作，宾汉(Bingham)指出，早期的胶体化学家认为，胶体化学之粘度计犹如电气科学之电流计，胶体化学家注意到，胶体的粘度随剪切和流动的时间而变化。粘度随剪切速率而减少的事实为宾汉和格林(Green)所证实，宾汉发现，悬胶体实质上是具有屈服值的软固体，在屈服值之外，形变速率随所施加的应力和屈服应力之间的差呈线性变化。然而1928年沸路(Farrow)等人对聚合物溶液的深入研究表明，宾汉的维持线性关系的试图是不真实的，粘度随剪切速率而减少的现象被奥斯瓦尔特(Ostwald)称之为构化粘度(Strukturviskositut)，被威廉逊(Williamson)称之为假塑性(Pseudoplasticity)，被雷拿(Reiner)称之为非牛顿。1928年，贺佐(Herzog)和韦森伯(Wrisenberg)论证了悬胶体和聚合物溶液在流动期间的弹性能和弹性回复。1933年，门尼(Mooney)测量了橡胶流动中的弹性回复以及对正弦振动的应力响应。另一种现象就是在流体中表观粘度随起始材料形变程度的增加而减少，这种现象被费兰特列茨(Freundlich)称之为触变性(thixotropy)，反之，流体粘度随剪切速率增加而增加的现象称之为触稠性(dilatancy)。1925年，奥斯瓦尔特首先发现聚合物溶液的粘度对剪切速率的依赖性。1929年，雷拿指出，在非常低的剪切速率下粘度有一个常值η0，直至特征的剪切速率范围，然后随第2特征剪切速率范围稳步地下降，在此范围以上，粘度维持一个常值η∞，从1933年至1936年，荻仑(Dillon)等测量了天然橡胶及其他化合物熔体粘度，这是首次对聚合物熔体的粘度进行测定，结果表明了橡胶熔体的非牛顿粘性特征。迪伦(Dillon)认为在橡胶－碳黑化合物中存在着屈服值，并用标志物显示了流动图案，在此期间，门尼首次精确测定了天然橡胶的剪切粘度。
在1920～1940年对流变学的研究集中在非牛顿剪切粘度和触变性行为。但在此期间也注意到了弹性性质，对微小振动作出响应的动力学粘度的定量研究也由菲利波夫(Philippoff)开始。1948年，佛罗里(Flory)等研究了聚合物的零剪切粘度和分子量之间的关系，从1955年到1957年，波列(Pollett)、菲利波夫等对法向应力的测定作了早期的工作，在板盘和圆锥之间流动的聚合物熔体或溶液会引起压力随半径的减少而增加的现象，引起这种现象的原因是法向应力差的存在，如果把方向“1”表示为速度分量方向；方向“2”表示为速度变化方向；方向“3”表示为等同方向，则τ11－τ22表示第1(主)法向应力差，τ22－τ33表示第二(次)法向应力差，在聚合物加工过程中，例如纺丝、吹膜、压模、注塑等，经常遇到拉伸的问题，由此引起流变学家的注意。1965年，玻尔曼(Ballman)研究了聚合物的拉伸粘度。1980年，怀特(White)等发现，聚合物的拉伸粘度与分子量分布有关，对于液晶高分子流变性质的研究始于1981年韦斯板仑(Wissbrun)等对液晶聚合物的熔体进行了粘度的测量，发现大多数热致性液晶聚合物的流动曲线都出现两个屈服点，形成所谓三区域流动(Three-zone flow)，这显然是与热致性液晶聚合物在加热过程中出现两处转变峰有关。对聚合物熔体和溶液流变性质的研究的一个很重要的方面就是用数学模型描述聚合物体系受外力作用时的响应，这些响应包括上述所有的现象，经过流变学家几十年的努力，现在已导出种类繁多的数学模拟公式，即“本构方程”。所谓本构方程就是描述物体受力失去平衡态时材料的响应，外加刺激作用与所导致的响应之间的关系是物质结构状态唯一的特征、因此称为本构方程、关于聚合物熔体的本构方程有多种描述。1958年由克里敏尼尔(Criminale)、依力克辛(Ericksen)和菲利(Filley)共同研究得出的本构方程称之为CEF方程，具体形式为
式中：η、ψ1、ψ2分别为粘度、第1法向应力差系数和第2法向应力差系数，它们都是应变速率张量数值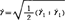
的函数，CEF方程有预测稳定剪切流中法向应力差的能力，应用CEF方程的关键是确定ψi和ψ2、伯特(Bird)等人推导出计算ψ1(
)的方程：
式中K是实验常数，在流变函数的实验确定中经常使用是毛细管和锥一板几何结构。1975年落茨(Lodge)改进了设计，利用“孔压误差”，使得有可能测量稳定测粘流动状态下的η、ψ1和ψ2，如果把法向应力差系数函数ψ1和ψ2略去不计，CEF方程就简化为广义牛顿流体方程或GNF方程：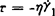
(3)
称之为G-M本构方程
式中
是应变(速率梯度)的共旋转速率，对于小变形流动
，由G-M方程给出一般线性粘弹性(LVE)流体。
式中G(t－t′)是松驰模量，它能取依赖于模拟真实LVE行为的LVE“力学模型”的具体形式，设想聚合物具有“双重性”，即具有牛顿粘性流体和虎克弹性固体这两种特性，并且这种双重性质同时起作用。例如：既然麦克斯韦(Maxwell)单元以剪切应力松驰实验为条件的，对t=0，r=0；对t＞0，r=r0，因此导致应力的时间依赖为
τ(t)=γ0Ge－t／λ (6)
式中松驰时间入是麦克斯韦单元的“粘度”与“模量”的比值，方程(6)能用来定义松驰模量的时间依赖：
式中H(lnλ)为连续松驰谱的函数。
GNF方程是一系列为解析流体非牛顿行为而建立起来的经验方程，半经验方程、或基于分子观念建立的一般表达。这些本构方程包含了粘度函数η对外加(或引起的)应变速率依赖性的不同表达方法，有如下的几种模型：幂律模型：
(11)
式中，m－参数(N·sn／m2)，n－幂律指数。由此可得幂律本构方程：
(12)
m是个温敏函数，服从阿伦尼乌斯(Arrhenius)型关系：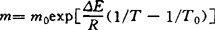
，△E为流动活化能
依力士(Ellis)模型
其本构方程为：
(14)
这个方程用剪切应力的数值来表达粘度，式中η0是零剪切粘度，τy2是η=η0／2处的剪切应力值
(a－1)是lg(η0／η－1)与lg(τ／τy2)关系曲线的斜率。加利亚(Carreau)模型
这个方程在它的非牛顿粘度预测上也很成功，并且便于使用。
宾汉(Bingham)流体。
式中τy为特征屈服应力
对于聚合物的拉伸粘度的数学描述和实验方法经近10年来流变学家的努力已日趋完善，对于稳态拉伸流动，τ22=τ33，由下式给定
式中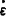
为拉伸速率，对简单拉伸流动
；
。对于平面拉伸流动(纯剪切流动)
。对于双轴拉伸流动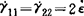
；
。
式中：F1为引起简单拉伸流动所需要的力，A1为与流动垂直的横截面面积。由于τ22=τ33=－Patm，因此实验上的拉伸粘度变为
从数学上推导得
，即拉伸粘度为剪切粘度的3倍，这一推导已为梅斯拿(Meissner)、玻尔曼(Ballman)、史蒂芬逊(Stevenson)、以及怀特(White)等人的实验所证实。由于电子计算机的应用和计算技术的发展，使得现代的流变学家能借助电子计算机对聚合物的复杂的流变行为进行模拟计算。从而指导工程设计、产品设计等。1990年，韩式方介绍了计算解析法在粘弹流体力学中的应用，他应用“准衰退记忆”原理，发展了一类拉伸流动的扰动本构理论，并在此基础上发展了拉伸流动稳定性的本征值理论，同年，金日光首先提出了有关非线性群子统计理论的物理表征值－组成之间关系的普遍方程，并具体考虑了各种二元高分子的表观粘度－组成、模量－组成关系曲线，计算曲线与实验值是相一致的。自从1975年天拿(Tanner)等首次用有限元法成功地求解非牛顿流体的挤出流动以来，数值模拟已成为一个热门的课题。1985年以来唐国俊等开展了松驰时间谱的数值分析、高聚物挤出流动中热传导的数值模拟等课题的研究，并取得了颇为有用的结果，在聚合物流变学领域中还有很多有待解决的难题，诸如各种本构方程的准确性，各种数值模拟与实验值的拟合性等问题还有测量各种流变性质的仪器、方法和改进等有待今后流变学家的努力。
(中国科学院广州化学研究所陈家楠研究员撰)