【机构结构及组成】
对机构结构的研究，是揭示机构内部构造的属性及其与机构运动学、动力学的基本内在联系。机构结构研究有结构描述及结构分析两部分内容。机构结构的描述是用一定的力学参数和构件、尺度等以及构件的联接方式表示机构的构造以识别机构。机构结构的分析包括机构运动自由度及约束特性的研究。
机构组成原理则是在给定结构参数、机构自由度、构件数、运动副类型条件下求机构的类型综合，以期改进现有机构及开发新机构。关于机构结构及组成的研究工作，1875年勒洛(F．Realeaux)曾给机构下了确切的定义，他系统地研究了组成机构的运动副，以及机构是由构件、运动副相联接而成的机构组成的最基本的概念。1887年高赫曼(X．Ц．Тохмaну)发表了关于啮合原理的论文。1869年契贝谢夫(П．Л．чебышюев)发表了平面机构结构公式。后来格吕布勒(M．GrÜbler)作为强制运动的准则导出。1887年沙莫夫(П．и．Cомов)发表了空间运动链结构公式，该公式在1923年由马雷谢夫(А．П．Мaьㄧщев)加以发展。1916年阿苏尔(A．B．Ассyp)发表了关于机构组成的理论，提出机构是将自由度为零的杆组依次联接到主动构件及机架上所组成的原理。阿苏尔同时提出了杆组分类的原始观点。在1939年阿尔托波列夫斯基(И．И．Арtоgоnвскцц)提出的机构分类法亦是基于杆组的分类。1951年巴拉诺夫(Г．Г．Бaрaнов)提出了巴氏木
架的概念，并提出了巴氏分类的观点。1943年多布罗沃尔斯基(B．B．Добровоaλьскuù)和阿尔托波列夫斯基发表了各族机构的统一结构公式。即根据加于组成机构的闭链中公共约束数的不同将机构分为5个族(类)，这个公式仅适用于单闭链及各闭链中公共约束数相同的机构。关于机构类型综合方面，1955年哈恩(K．Hain)发表了平面转动副组成的八杆单自由度机构有16种。机构结构与组成原理研究现况如下1．机构结构的描述：除了原有的机构运动简图表示法有弗伦克标记法、图论表示法、矩阵表示法。矩阵表示法有关联矩阵、卸接矩阵、D-H矩阵、回路矩阵、结构矩阵等，这种方法可表示较多的结构信息，可直接用于机构建模并易于计算机作数学处理。码表示法包括最优码、最小码、度码、分层码、邻度码、关联度码等。这种方法的最大特点是紧凑，往往只需一个数即可表示机构中的联接关系，故便于比较。码表示法主要于机构的同构识别。机构结构的识别包括同构判定与结构类型识别两部分内容。机构的同构判定主要有3类方法：特征多项式法：运算效率高，但不具有唯一性；码法：唯一性好，但运算效率低；关联表法：如路径码、标识码等。机构同构判定问题运用码法已基本解决，现主要的研究方向是提高运算效率。机构的结构类型识别应在同构判定的基础上再根据机构中运动副间的几何关系进行，这方面的系统研究尚未见报道。2．机构结构的分析(1)计算机构活动度的基本公式为：
其中fi为机构中第i个运动副的相对自由度，ξj为第j个回路中的ξ值。ξ是回路的闭合约束，是回路中独立约束方程式的数目；根据单闭链结构与其ξ值的关系可以确定机构中各回路中的ξ值，从而求得机构的活动度。
(2)机构中活动度的类型。机构的活动度可分为3种类型：完全活动度，部分活动度及可分活动度。对于不太复杂的平面机构不难用直观法靠人工观察机构的简图判定。另外可以用矩阵法及结构分解法进行判断。对于平面机构的活动度类型判定已有充分的根据，尚有必要研究一般机构活动度判定的充要条件。(3)机构的约束特性。机构的实际约束方程数可分为全周期与瞬时两种。对于全周期的约束方程数，分析的方法主要是位移方程分析法，这种方法需对机构的位移方程组进行独立性分析。由于位移方程的非线性，这项工作极为困难。对于瞬时约束方程数，主要方法有矩阵求秩法及末杆自由度分析法，这种方法通过分析单开链末杆自由度，再闭合成闭链得到回路的约束方程数。相对说来，机构瞬时约束方程数较易确定。(4)过约束机构。机构根据其约束特性可分为3种类型：①无过约束机构：这时ξ值只取决于机构中的类型与数目，ξ=f，F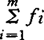
，F＜6，或ξ=6(当F≥6时)。②一般过约束机构：这时ξ值不仅取决于机构中的运动副类型与数目，还取决于运动副间的几何关系(同轴、平行、相交、共面、垂直、任意)，此时ξ＜min(F，6)。③特殊过约束机构：这时ξ值不仅取决于以上轴线位置的几何关系，还取决于机构几何尺度间的特定关系，此时ξ＜min(F，6)。实用机构绝大多数属于前两种类型。(5)机构奇异位移。若在机构的某一位形，机构的ξ值变小，则机构位于奇异位形，在实际工作中常需要确定机械手的所有奇异位形。当机械手田雅可比矩阵降秩时机械手处于奇异位形。也可以用螺旋运算，当机械手在某一位置螺旋系阶数降低即为奇异位形。(6)消极约束及冗余自由度。消极约束是由于机构中回路与回路间的约束存在相关性产生的，它往往与机构中回路的相似、对称、平行等及具体尺度有关。目前消极约束的存在的确定尚未很好解决，在实际中要根据具体情况分析。冗余活动度在单回路中单构件或多构件间的冗余活动度常称为多余自由度。在多回路机构中的冗余活动度可能存在于子链结构中。3．机械的组成：(1)机构的结构类型综合：这是在给定结构参数下求所有可能结构形式的过程。机械结构类型的综合的重点是多回路机构的结构类型问题。对平面运动链已解决了10杆单自由度机构得230种，8杆杆组得173种。目前已发展到含复合铰链的运动链的综合研究。空间机构的类型综合已得到由P、R、C副组成的单自由度单闭链的类型综合。(2)机械类型优化问题的研究：这方面的工作以机械手的结构研究最为系统深入。同时已有不少实用机构根据这个思路进行了实例研究，取得了良好的效果。机构结构及组成研究展望1．探讨更完善的机构结构描述方法，以利于更好地揭示机构的结构与性能间的关系。2．实现任意机构分析的计算机自动生成，在给定机构结构信息之后，计算机自动确定各回路的ξ值。自动计算活动度并判别其类型。自动建立机构的运动学与动力学方程并求解。3．实现机构类型优化综合的研究。结合生产实际开发新机构应成为机构学研究的一个重要内容。由于满足功能要求的机构结构方案数众多，其评价准则往往是经验性知识，因而要进一步发展到机构综合的专家系统。【参考文献】：1 Ассурсцссuaнпе ∧ B．Cмрсиеьх Мехaнiзиоь，Usg．AHссср，19522 Aрмобоцбcкцǚ Ц Ц．Гео／ща Механцжцоб Ц МаццuнюТНТТA，19513 Davies T H，Crossley F R E．Structural Analysis of Plane Linkages by Frank’es Condensed Notation，J of Mechanisms，Vol．1，19664 Dobrjanskyj L，Freudenstein F．some Applications of Graph Theory to the Structual Analysis of Mechanisms，Trans，ASME，J of Engr．for Industry，19675 Mruthyuu u jaya T S，Raghavan M R．Structual Analysis of Kinematic Chains and Mechanisms Based on Matrix Representation，Trans．ASME，J of Mech Design，Vol．1 01，19796 Luo Yu-Feng，Yang Ting-Li，Cao Wei-Qing．Identification of Spatial Kinematoc Chains Using Incident Dcqree and Incident Degree Code，Proc．of 8th World Congress on Theory of Moch and Mech．19917 Freudenstein F，Alizade R．On the Degree of Freedom of Mechanisms with Variable General Constraint，Proc．of 4th World Congress on the Theory of Mech and Mech．19758 Yang Tingli，et al．Topological Characteristics and Automatic Generation of Structural Analysis and Synthesis of plant Mechanisms，Traeds and Developments in Hechanisms，Machines，and Robotics，Vol．1，19889 Dimentberg F M，et al．A Spatial Four-Link Mechanism Having Two Prismatie Pairs，Mech and Mech．Theory．1966，110 张启先．空间机构分析与综合(上册)．北京：机械工业出版社，1984(陕西机械学院曹惟庆撰)