The rate of change of direction of a curve at a point on the curve. The Greek letter κ‎ is used to denote curvature, and for a planar curve y(x) is given by $\text{κ}=\frac{\left|y″\right|}{{\left(1+{\left(y’\right)}^2\right)}^{3/2}}$. A curve with constant non-zero curvature κ‎ is a circle of radius 1/κ‎; a curve with zero curvature is a line. $\rho =\frac{1}{\kappa }$ is the radius of curvature which is the radius of the circle which best fits the curve at that point, matching the position, the gradient, and the second derivative of the curve at that point. The centre of curvature is the centre of that best-fitting circle, known as the circle of curvature. The locus traced out by the centres of curvature is called the evolute.

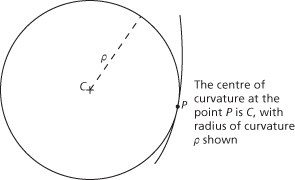
The centre of curvature at the point P is C, with radius of curvature ρ‎ shown

See also Serret-Frenet formulae.