A set of polynomials {pk(x)}, k ≥ 0 are said to be orthogonal over an interval [a,b] if for some positive weighting function w(x),
when i ≠ j. See Chebyshev polynomials, Hermite polynomial, Legendre polynomials.
Polynomials designed to simplify calculations when a response variable is believed to be related to a polynomial function of an explanatory variable. If x1, x2,…, xn are n observations on the variable X, then the polynomials Φ1(x) and Φ2(x) are orthogonal if
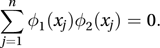 If we wish to fit the model
If we wish to fit the model then we will need (see multiple regression model) to invert the matrix product X′X, where
then we will need (see multiple regression model) to invert the matrix product X′X, where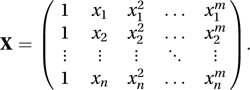 This may not be easy, since X′X will often be nearly singular. One solution is to rewrite the model in the form
This may not be easy, since X′X will often be nearly singular. One solution is to rewrite the model in the form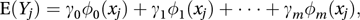
where Φ0(x)=1 and Φk(x) is a polynomial of degree k (k=1, 2,…, m). With n observations on x, denoted by x1, x2,…, xn, the polynomials are chosen to be orthogonal, i.e. to satisfy the requirements that
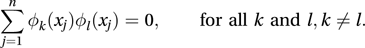 The revised X matrix has a typical element Φk(xj) and is such that the product X′X is now a diagonal matrix and is therefore easily inverted.
The revised X matrix has a typical element Φk(xj) and is such that the product X′X is now a diagonal matrix and is therefore easily inverted.Often the appropriate degree of dependence on x (in other words, the value of m) is unknown. The reformulation also makes it easy to select an appropriate model without the need for further iterations. In the ANOVA table the contributions for each polynomial can be listed separately.
- International Organization for Standardization
- international payments
- International Polar Year
- International Practical Temperature Scale
- International Programme of Ocean Drilling
- International Research Institutions for Seismology
- international reserves
- Internationals
- International Scientific Optical Network
- International Society for Bayesian Analysis
- International Society for Clinical Biostatistics
- International Space Company Kosmotras
- International Space Station
- International Space University
- International Standard Classification of Occupations
- International Standards Organization
- International Statistical Institute
- International Statistical Review
- International Sunspot Number
- International Sun–Earth Explorer
- international system
- International Telecommunications Satellite Organization
- International Telecommunication Union
- International Terrestrial Reference Frame
- International Thermonuclear Experimental Reactor