For a random variable X, the cumulative distribution function (or cdf) is the function FX defined by FX(x) = Pr(X ≤ x). Thus, for a discrete random variable,
where pX is the probability mass function, and, for a continuous random variable, with a probability density function fX, then
The function F, for a random variable X, defined for all real values of x by
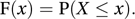 Clearly, F(−∞)=0, and F(∞)=1, where F(−∞) and F(∞) are the limits of F(x) as x tends to −∞ and ∞, respectively. This function is a non-decreasing function such that if x2>x1 then F(x2)≥F(x1). If X is a continuous random variable then F is a continuous function, and conversely. If X has probability density function f then
Clearly, F(−∞)=0, and F(∞)=1, where F(−∞) and F(∞) are the limits of F(x) as x tends to −∞ and ∞, respectively. This function is a non-decreasing function such that if x2>x1 then F(x2)≥F(x1). If X is a continuous random variable then F is a continuous function, and conversely. If X has probability density function f then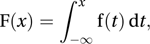 and f(x)=F′(x), where F′(x) denotes the derivative of F(x).
and f(x)=F′(x), where F′(x) denotes the derivative of F(x).A useful property of F is that, for any value of x, there is a corresponding value u, 0≤u≤1, such that
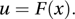
In the case where F is a continuous and increasing function for a≤x≤b, the random variable U defined by U=F(X) has a continuous uniform distribution on the interval 0≤u≤1, and, for a given value of U, the corresponding value of X is given by F−1(U). See simulation.
In the case of a discrete random variable, the distribution function is a step function, in which the step at xj is P(X=xj), and F(x) → F(xj) as x → xj from above, but F(x) → F(xj−1) as x → xj from below.
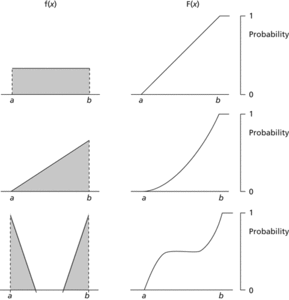
Cumulative distribution function. In each example the probability density function f defined in the interval (a, b) is shown on the left, with the corresponding cumulative distribution function F on the right. The scale from 0 to 1 refers to F.
See probability distributions.
The cdf of a random variable X at point x is the probability that X takes values at or below this point. Hence, F(x) = P[X ≤ x]. The following properties must hold for any cdf: it is a non-decreasing right-continuous function; it tends to 0 at minus infinity and tends to 1 at plus infinity.
- polarity event
- polarity excursion
- polarity interval
- polarity reversal, geomagnetic
- polarity subchron
- polarity subchronozone
- polarity subzone
- polarity superchron
- polarity superchronozone
- polarity superzone
- polarity timescale
- polarity transition period
- polarity zone
- polarizability
- polarization
- Polarization & Anisotropy of Reflectances for Atmospheric Sciences coupled with Observations from a Lidar
- polarization colours
- polarization diversity
- polarization, electrode
- polarization of light
- polarized plug
- polarized radiation
- polarized relay
- polarizer
- polarizing angle