An alternative to a moment as part of a summary of the form of a distribution. If the moment-generating function of a distribution exists, then its natural logarithm exists and is called the cumulant-generating function (cgf). The coefficient of t^r/r! in the Taylor expansion (see Taylor series) of the cgf is called the rth cumulant and is denoted by κ_r (where κ is kappa). The cumulants can be expressed in terms of the central moments, and vice versa. In particular, denoting the mean by μ and the moments by μ₂, μ₃,…,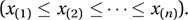For an example of the application of cumulants, see cornish–fisher expansion. The term ‘cumulant’ was introduced by Sir Ronald Fisher and Wishart, following a suggestion by Hotelling.