The following is a summary of some of the theorems that are concerned with properties of a circle:

1. (i) Let A and B be two points on a circle with centre O. If P is any point on the circumference of the circle and on the same side of the chord AB as O, then ∠AOB = 2∠APB. Hence the ‘angle at the circumference’ ∠APB is independent of the position of P.

2. (ii) If Q is a point on the circumference and lies on the other side of AB from P, then ∠AQB = 180°-∠APB. Hence opposite angles of a cyclic quadrilateral (see cyclic polygon) add up to 180°.

3. (iii) When AB is a diameter, the angle at the circumference is the ‘angle in a semicircle’ and is a right angle.

4. (iv) If T is any point on the tangent at A, then ∠APB = ∠BAT.

5. (v) Suppose now that a circle and a point P are given. Let any line through P meet the circle at points A and B. Then PA. PB is constant; that is, the same for all such lines. If P lies outside the circle and a line through P touches the circle at the point T, then PA.PB = PT².

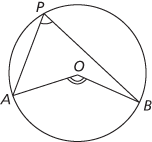
(i) ∠AOB = 2∠APB

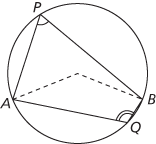
(ii) ∠AQB = 180°−∠APB

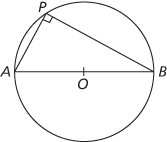
(iii) A diameter subtends a right angle

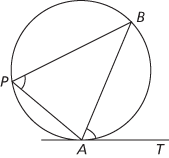
(iv) ∠APB = ∠BAT

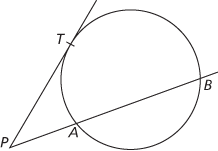
(v) PA.PB = PT² is constant