A closed curve every point on which is a fixed distance (the radius) from a point (the centre) within the curve. The diameter is a line that joins two points on the circumference and passes through the centre: the diameter is twice the radius (r). The circumference of a circle is equal to 2πr; the area is πr2, where π is a constant with the value 3.141 592. In analytical geometry the equation of a circle, centred at the origin, is x2+y2=r2.
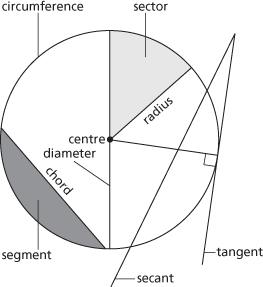
Circle.
The circle with centre P and radius r is the locus of points in the plane whose distance from P is equal to r. If P has Cartesian coordinates (a,b), this circle has equation (x−a)2 + (y−b)2 = r2. An equation of the form x2 + y2 + 2gx + 2fy + c = 0 represents a circle if g2 + f2−c > 0 and is then an equation of the circle with centre (−g,−f) and radius .
The area of a circle of radius r equals πr2, and the length of the circumference equals 2πr.
- propenoate
- propenoic acid
- propenol
- propenonitrile
- propensity
- propensity score
- propensity score matching
- propensity to consume
- propensity to save
- propenyl group
- proper ancestor
- proper class
- proper divisor
- proper factor
- proper fraction
- proper map
- proper motion
- proper names
- proper subgraph
- proper subset
- properties
- proper time
- property
- property company
- property developer