A function that relates a joint cumulative distribution function to the distribution functions of the individual variables. If the individual distribution functions are known, but the joint distribution is unknown, then a copula can be used to suggest a suitable form for the joint distribution.
Let F be the multivariate distribution function for the random variables X1, X2,…, Xn and let the cumulative distribution function of Xj be Fj (for all j). Define random variables U1, U2,…, Un by Uj=Fj(Xj) for each j, so that the marginal distribution of each Uj has a continuous uniform distribution in the interval (0, 1). Assume that for each value uj there is a unique value and let the joint cumulative distribution function of U1, U2,…, Un be C. Then for all u1, u2,…, un in (0, 1), since Uj<uj if and only if Xj<Fj−1(uj). The function C is called the copula. An equivalent equation to the above is
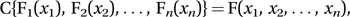 for all x1, x2,…, xn , where uj=Fj(xj) for each j. Sklar's theorem, formulated by Abe Sklar of the Illinois Institute of Technology and published in 1959, states that, for a given F, there is a unique C such that this equation holds.
for all x1, x2,…, xn , where uj=Fj(xj) for each j. Sklar's theorem, formulated by Abe Sklar of the Illinois Institute of Technology and published in 1959, states that, for a given F, there is a unique C such that this equation holds.Note that it may well be that it is not possible to express the inverse functions Fj−1 in a simple form (an example is the multivariate normal distribution).
Assuming that the copula and the marginal distribution functions are differentiable, the corresponding result for probability density functions is that
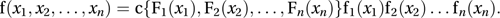
The trivial case where c {F1(x1), F(x2),…, F(xn)}=1 corresponds to the case where the n X-variables are independent. Thus the copula encapsulates the interdependencies between the X-variables and is therefore also known as the dependence function. If c(u1, u2,…, un) is the joint probability density function of U1, U2,…, Un, then
 where , for each j.
where , for each j.
In traditional logic a proposition not only contains a subject and a predicate, but also a coupling device or copula (is, are, is not, are not) binding them together. It is generally held that very different things are covered by the notion, such as the ‘is’ of predication (rain is wet), that of identity (Marilyn Monroe is Norma Jean), and that of composition (this statue is marble). The need for a copula arises from a picture in which all the other elements of a proposition are complete ‘terms’, so they need some glue to bind them together into a sentence. Since Frege it has been more common to think of the predicate in a subject-predicate sentence on the model of an expression for a mathematical function, which needs no coupling device to bind it to its argument. No such connection has to be postulated, any more than there is a connection between the square function and 2 in the expression 22.
- Nigerian Civil War
- Nigerian fraud
- NigeriaSat-2
- NigeriaSat-X
- Niggli method
- Niggli, Paul (1888–1953)
- nightglow
- nightingale
- Nightingale, Florence (1820–1910)
- Night of the Long Knives (29–30 June 1934)
- night sky brightness
- night vision
- night vision system
- nihil in intellectu nisi prius in sensu
- nihilism
- nihonium
- Nijmegen, Treaty of (1678)
- Nikkei index
- Nikolayev, Andrian Grigoriyevich (1929–2004)
- NIL
- Nile, Battle of the (1 August 1798)
- nilpotent
- nilradical
- Nilson, Lars Fredrick
- nimbo-, nimbus