The convex hull of a subset S of n-dimensional space is the smallest convex set containing S. The convex hull of 3 not collinear points is a triangle, of 4 not coplanar points is a tetrahedron. (See simplex).
The convex hull of a set of points in ℝn is the smallest convex polyhedron (polygon when n=2) that contains all the points.
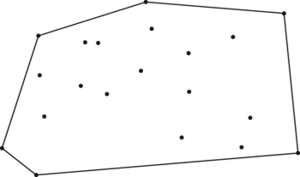
Convex hull. The hull is defined by the positions of the extreme points. In two dimensions the hull is a convex polygon.
The smallest convex set that contains a given set. A set is convex if for any two points in the set, the points on the straight line segment joining the two points are also contained in the set.
- Rainwater, (Leo) James
- raised beach
- raised bog
- raised cosine window
- raise(to a power)
- Rajagopalachariar, Chakravarti (1878–1972)
- Rajput
- rake
- Raketoplan
- raking
- Rakosi, Matyas (1892–1971)
- RAL
- Raleigh, Sir Walter (1552–1618)
- RAM
- r.a.m.
- Ramachandran plot
- Ramakrishna movement
- Raman effect
- Raman, Sir Chandrasekhara Venkata
- Ramanuja (1137)
- Ramanujan, Srinivasa (1887–1920)
- Ramanujan, Srinivasa Iyengar
- Ramapithecus
- Ramaty High-Energy Solar Spectroscopic Imager
- Rambouillet, Catherine de Vivonne, Marquise de (1588–1665)