The extension of the linear regression model to the case where there is more than one explanatory variable (see regression). For the case of p X-variables and n observations the model is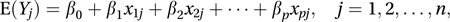where β₀, β₁,…, β_p are unknown parameters. An equivalent presentation is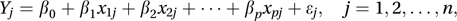where ε₁, ε₂,…, ε_n are random errors.

In practice the explanatory variables may be related as in the quadratic regression model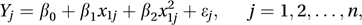the cubic regression model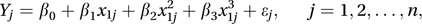and the general polynomial regression model (also termed a curvilinear regression model)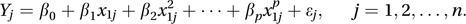

In matrix terms the model is written as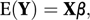where Y is the n×1 column vector of random variables, β is the (p+1)×1 column vector of unknown parameters, and X is the n×(p+1) design matrix given by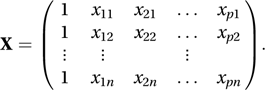Equivalently,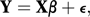where ɛ is an n×1 vector of random errors.

Usually it is assumed that the random errors, and hence the Y-variables, are independent and have common variance σ². In this case, the ordinary least squares (see method of least squares) estimates (see estimator) of the β-parameters are obtained by solving the set of simultaneous equations (the normal equations) which, in matrix form, are written as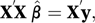where X′ is the transpose (see matrix) of X and y is the n×1 column vector of observations (y₁ y₂…y_n)′. The matrix X′X is a symmetric matrix. If it has an inverse then the solution is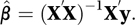

The variance-covariance matrix of the estimators of the β-parameters is σ²(X′X)⁻¹. The Gauss–Markov theorem shows that β is the minimum variance linear unbiased estimate of β̂.

If the random errors are not independent or have unequal variances then ordinary least squares is inappropriate and weighted least squares may be appropriate. If the random errors are influenced by the X-variables, then a possible approach is to identify (if possible) W-variables that are highly correlated with the X-variables, but not with the errors. These W-variables are called instrumental variables. The subsequent analysis, commonly used in econometrics, uses two-stage least squares, in which the first stage involves the regression of the X-variables on the W-variables to obtain fitted values:

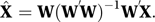
These values are then used in place of the X-values in the regression for Y to give the estimate β̂₂:

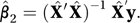
A perennial problem with multiple regression models is deciding which of the X-variables are really needed and which are redundant.

A related problem is that of collinearity (or multicollinearity). Suppose, for example, that the two explanatory variables X_j and X_k approximately satisfy the relation X_j=a+bX_k. In this case a multiple regression model that involves both X_j and X_k will run into problems, since either variable would be nearly as effective on its own. The situation can arise with other numbers of X-variables: in all cases the result is that the matrix X′X is nearly singular. The equation X′Xβ̂=X′y is then said to be ill-conditioned. One suggestion is to replace the usual parameter estimate by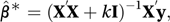where k is a constant and I is an identity matrix. This technique is called ridge regression. A plot of the elements of β̂* against k is called a ridge trace and can be used to determine the appropriate value for k. The estimates of the β-parameters obtained using this method are biased (see estimator) but have smaller variance than the ordinary least squares estimates.

When there are many X-variables interpretation of the fitted model can be difficult and there may be several variables whose importance is questionable by reason of the small values of the corresponding β-parameters. A procedure that usually results in many of these β-parameters being set to zero (so that the corresponding explanatory variable is removed) is the lasso, in which the usual estimation procedure (see method of least squares) is modified by the restriction that

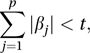
where t is a tuning constant (see M-estimate).

For methods of evaluating the fit of a multiple regression model, see regression diagnostics. See also model selection procedure; stepwise procedure.