A test suitable for the simultaneous testing of hypotheses concerning the equality of three or more population means. When samples have been taken from several populations, a question of interest is whether the populations all have the same mean. In the case of m populations, with the mean of population j denoted by μ_j, the null hypothesis is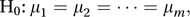with the alternative being that H₀ is false.

In the simpler case m=2, an appropriate test statistic (assuming the populations have the same variance) is T given by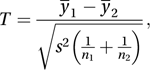where y¯_j is the mean of the n_j values sampled from population j, and s² is the pooled estimate of the common variance (see pooled estimate of common mean). The statistic T has an approximate t-distribution with ν=(n₁+n₂−2) degrees of freedom (the approximation is exact for samples from normal distributions). Denoting the upper 100α % point of a t-distribution with ν degrees of freedom by t(α, ν), H₀ is rejected at the 200α % level if |T|>t(α, ν).

In the case of m populations, the null hypothesis can be rewritten in the form: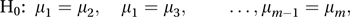which demonstrates that there are c=½m(m−1) pairs of populations that could be compared. However, if c independent t-tests are performed, each at the 100α% level, then the overall significance level is 1−(1−α)^c and is not α.

In the case of equal sample sizes (all n), the quantity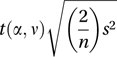is called the least significant difference (LSD). If no differences are greater than this, then H₀ may be accepted at the 100α% level.

One way of reducing the overall significance level is to reduce the value of α for the individual tests. The Bonferroni inequality leads to the replacement of α by α/c: the resulting test is variously known as the Dunn test or as the Bonferroni t-test. A preferable alternative uses the Sidak correction, in which α is replaced by 1−(1−α)^1/c. However, both tests have rather low power (see hypothesis test) when m is large. A more relaxed approach involves controlling the false discovery rate, rather than the overall significance level.

Tukey suggested using the Studentized range distribution in place of the t-distribution. The resulting test is familiarly called either the Tukey test, the honestly significant difference test, or the HSD test. This test assumes equal sample sizes; modifications for unequal sizes are the Tukey–Kramer test which uses (1/n_i+1/n_j) when comparing populations i and j, and the Spjotvoll–Stoline test which uses 2/n_s, where n_s is the smallest of the m sample sizes. The Tukey tests are probably the best choices of all the multiple comparison tests. Similar in spirit to the Tukey tests are the Hochberg test and the Gabriel test; their test statistics are compared with the distribution of the maximum absolute value rather than with that of the Studentized range. The Waller–Duncan test is a test based on the F-test (see test for equality of variance) for overall differences between treatments.

An alternative to comparing all pairs simultaneously is to use a multistage test. Suppose that the samples are labelled in order of their means, so that sample 1 has the least mean and sample m the greatest mean. Initially all m samples are compared. If H₀ is accepted, then testing ceases. However, if it is rejected, then the hypotheses μ₁=μ₂=…=μ_m−1 and μ₂=μ₃=…=μ_m are considered, using the Studentized range values for the comparison of m−1 populations. If a hypothesis is rejected, then comparisons of m−2 populations are made. Successive reductions are made until acceptable hypotheses are found. Examples of this type are Duncan’s test (which uses the significance level 1−(1−α)^l−1 when l means are compared), the Newman–Keuls test (which uses α throughout), and the Ryan–Einot–Gabriel–Welsch (R–E–G–W) test which uses 1−(1−α)^l/m for l<m−1 and α otherwise. A compromise between the Newman–Keuls test and the HSD test is the Tukey wholly significant difference test, which is also called the WSD test or Tukey b-test.

When one of the m populations under comparison is different to the remainder (for example, it refers to the use of a control treatment) then interest focuses on the (m−1) comparisons involving this population. In this case the Dunnett test is appropriate. The usual t-statistic is used, but with special tables of critical values. When the remaining m−1 treatments are ordered (for example, they represent different concentrations of some new substance) then the successive T-values will generally also be ordered and the number of tests reduced. This is known as the Williams test; revised tables of critical values are required. In yet another approach (the Hsu MCB test) attention is restricted to comparisons involving the best treatment.

If the comparisons of interest are contrasts (see ANOVA) of more than two population means then the Scheffé test, which is based on the F-distribution, is appropriate.

In cases where the variances differ from one population to another, variants on the above tests are required. For example, the Tamhane test uses the Welch statistic in place of T, together with the Sidak correction, while the Games–Howell test replaces the denominator of T by when comparing populations i and j and also modifies the number of degrees of freedom.