The distribution of the multinomial random variable which is the generalized form of the binomial distribution to allow more than two outcomes in each of the individual trials. So if {Yi}, i = 1, 2,…, n, is a series of independent, identically distributed random variables with Pr{Yi = xj}=pj for j = 1, 2,…, k with ∑pj = 1 then the probabilities of the possible outcomes are given by the coefficients in the expansion of (p1x1 + p2x2 + … + pkxk)n.
The extension of the binomial distribution to the case of m (>2) possible outcomes. Suppose that the probabilities of outcomes 1, 2,…, m are p1, p2,…, pm with . Let Xj denote the number, in a sample of size n, of occurrences of outcome j, for j=1, 2,…, m. The random variables X1, X2,…, Xm have a multivariate distribution given by
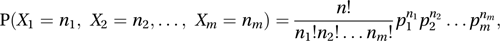where 0≤n1, n2,…, nm≤n and with . The random variable Xj has expected value npj and variance npj(1−pj) and the covariance of Xj and Xk (j≠k) is−npjpk. The term ‘multinomial distribution’ was introduced by Sir Ronald Fisher in 1925.
- Hapsburg
- hapten
- haptic
- haptic interface
- hapticity
- haptics
- haptonasty
- haptotropism
- haque
- Hara Takashi (1856–1921)
- Harbaugh, Gregory Jordan (1956– )
- Harberger triangle
- hard acid
- hard address
- hard base
- hard boot
- hard bounce
- hard budget constraint
- hard clipping
- hard copy
- hardcore process
- hard-core unemployed
- hard currency
- hard decision decoding
- hard disk