A means of describing the turning effect of a force about a point. For a system of coplanar forces, the moment of one of the forces F about any point A in the plane can be defined as the product of the magnitude of F and the distance from A to the line of action of F and is considered to be acting either clockwise or anticlockwise. For example, suppose that forces with magnitudes F1 and F2 act at B and C, as shown in the figure. The moment of the first force about A is F1d1 clockwise, and the moment of the second force about A is F2d2 anticlockwise. The principle of moments considers when a system of coplanar forces produces a state of equilibrium.
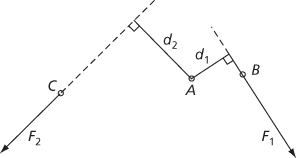
Moments about A
However, a better approach is to define the moment of the force F, acting at a point B, about the point A as the vector (rB−rA) × F, where × denotes the vector product and rA, rB are the position vectors of A and B. The use of vectors not only eliminates the need to distinguish between clockwise and anticlockwise directions but facilitates the measuring of the turning effects of non‐coplanar forces acting on a 3‐dimensional body.
Similarly, for a particle P with position vector r and linear momentum p, the moment of the linear momentum of P about the point A is the vector (r−rA) × p. This is the angular momentum of the particle P about the point A.
Suppose that a couple consists of a force F acting at B and a force −F acting at C. The moment of the couple about A is equal to
which is independent of the position of A.
- See, Elliott McKay, Jr (1927–66)
- seeing
- seek time
- seep
- seepage
- seepage velocity
- seesaw mechanism
- Sefström, Nils Gabriel
- Sega, Ronald Michael (1952– )
- Seger cones
- segment
- segmentation
- segmentation genes
- segmented labour market
- segmented market
- segmented mirror
- segregation
- segregation coefficient
- Segrè chart
- Segrè, Emilio Gino
- SEI
- seiche
- seif
- seif dune
- seigniorage