A non-parametric test of the null hypothesis that two populations have the same distribution, in the case where the distributions are continuous. Two independent random samples x₁, x₂,…, x_m and y₁, y₂,…, y_n are drawn and the test statistic is W, given by 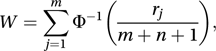where r_j is the rank of x_j when the (m+n) observations are arranged in increasing order of size, and Φ is the cumulative distribution function of the standard normal distribution. The restriction to continuous variables ensures that there are no ties. The test, proposed by van der Waerden in 1952, requires special tables.