The Cantor function C:[0,1]→[0,1] is an example of a continuous cumulative distribution function which has no probability density function. To define C, we write x∈[0,1] in ternary. If x’s expansion includes the digit 1, then all digits after the first 1 are made 0; any 2s are then made into 1s, and C(x) is this expansion, evaluated in binary. For example, any x in the range 7/9 < x < 8/9 has expansion x = 0.21…₃ and so C(x) = 0.11₂ = 3/4. See the sketch. The graph of C is sometimes called the Devil’s Staircase.

C is continuous everywhere and differentiable almost everywhere with derivative 0. In fact, C is not differentiable only on the Cantor set, which is a null set. So any pdf would be 0 almost everywhere, and hence no pdf exists. Note that $\underset{0}{\overset{1}{{\displaystyle \int }}}{C}^{\prime }\left(x\right)\text{d}x=0\ne 1=C\left(1\right)-C\left(0\right).$ This does not contradict the Fundamental Theorem of Calculus, as C′ is not continuous. C is uniformly continuous but is not absolutely continuous.

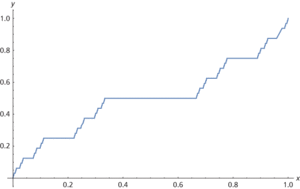
The Devil’s Staircase, the cdf of the Cantor distribution