A technique for partial differential equations with boundary conditions. For example, in the figure
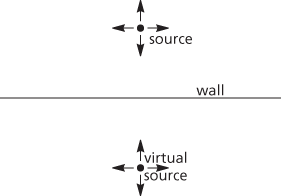
A bounding wall
there is a source in the upper half-plane with a wall or barrier along the x-axis. The boundary condition at the wall is that there is no flux through the wall. The solution in the upper half-plane might also be arrived at without the wall if there were a virtual source of equal strength at the source’s mirror image. This latter equivalent problem is then easier to solve.
Likewise, if a vortex was placed in the first quadrant, with walls along the positive x- and y-axes, then three virtual vortices—of equal strength, but two with opposite circulation—can be positioned appropriately in the other three quadrants so to meet the zero flux boundary conditions at the walls.
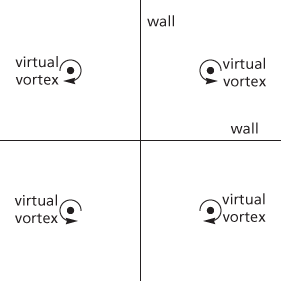
Two perpendicular bounding walls
A method of deriving field distributions where a large perfectly reflecting surface is present in the problem. Any source in the problem is duplicated on the other side of the surface at the same distance from the surface, by reflection. The surface can then be removed and the field distribution from this combined collection of sources is then the same as if the surface had been left in place.
- Cambridge equation
- Cambridge Platonists
- Cambridge Ring
- camcorder
- Camden, Battle of
- camel case
- Camelopardalis
- camera
- cameral
- cameral fluid
- camera phone
- camera ready
- Camerarius, Rudolph Jacob
- Camerata
- Cameron, David (1966)
- Cameron, Kenneth Donald (1949– )
- Cameroon
- Camisards
- camouflage
- cAMP
- Campaign for Nuclear Disarmament
- Campanella, Tommaso (1568–1639)
- Campanian
- Campbell-Bannerman, Sir Henry (1836–1908)
- Campbell bridge