1. The middle number of a set of numbers arranged in order. When there is an even number of numbers the median is the average of the middle two. For example, the median of 1,7,21,33,37 is 21, and of 1,7,21,33,37,54 is (21+33)/2=27.
2. A straight line in a triangle that joins the vertex to the mid-point of the base.
If a set of numerical data has n elements and is arranged in order so that either
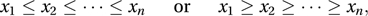 then the median is if n is odd, and if n is even.
then the median is if n is odd, and if n is even.For example, the time intervals (in minutes, to the nearest minute) between the eruptions of Old Faithful on 1 August 1978 were
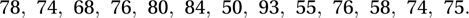
Arranging these thirteen values in order, we get
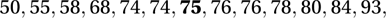 to give a median of 75 minutes. For 4 August 1978, there were fourteen inter-eruption times, which arranged in order were
to give a median of 75 minutes. For 4 August 1978, there were fourteen inter-eruption times, which arranged in order were so that the median is (73+75)=74.
so that the median is (73+75)=74.Alternatively, an approximate value for the median can be read from a cumulative frequency graph as the value of the variable corresponding to a cumulative relative frequency of 50%.
For a continuous random variable X, the median m of the distribution is such that P(X≤m)=. For a discrete random variable taking values x1<x2<…, the median is xi if P(X<xi)< and P(X>xi)<, and it is (xi+xi+1) if P(X≤xi)= and P(X≥xi+1)=. See also percentile; quartile.
A type of statistical average equal to or exceeded by half the values in a statistical distribution. The medium has the advantage that it is not influenced by extreme values and can be calculated from incomplete data. However, it cannot be used in any other form of mathematical processing. It is useful in quantifying data such as the statistical distribution of particle sizes.
See measures of location.
In signal statistics, the average value computed for each signal data point by taking it and a fixed number of its immediate neighbours and determining their median value. The median is found by sorting the values and taking the one in the middle.
The middle number or value in a series of numbers or values.
In statistics, the average as defined by the central value in a data set when the data set is ordered by value.
See mean (mathematical).
The median of the distribution of a random variable X is the value m such that P[X ≤ m] ≥ 1/2 and P[X ≥ m] ≥ 1/2. A median of a sample is an order statistic that gives the ‘middle’ value of the data, that is, the value such that there is an equal number of observations below and above it, if the sample size is odd, or the average of the two such central values, if the sample size is even. As a measure of central tendency of the data it is sometimes preferred to the mean, since it is not affected by outliers.