A form of symbolic logic, devised by George Boole (1815–64) in the middle of the 19th century, which provides a mathematical procedure for manipulating logical relationships in symbolic form. For example in Boolean algebra a+b means a or b, while ab means a and b. It makes use of set theory and is extensively used by the designers of computers to enable the bits 0 and 1, as used in the binary notation, to relate to the logical functions the computer needs in carrying out its calculations.
A set of elements defined with two binary operations (∨ and ∧), a unary operation (¬) and two elements 0 and 1 which possess the following properties:
(i) Both operations ∨ and ∧ are commutative and associative.
(ii) 0 is an identity for addition and 1 is an identity for multiplication.
(iii) Each operation ∨ and ∧ is distributive over the other.
(iv) a ∨(¬a) = 1 and a ∧(¬a) = 0 for all a.
For example, a power set ℘(X), where ∨ is union, ∧ is intersection, ¬ is complentation in X, and 0 is the empty set and 1 is X, is a Boolean algebra. Compare Boolean ring; see also Stone space.
The algebra, developed by Boole, of events (see sample space), unions, intersections and complementary events in a sample space S. For any events A, B, C the following algebraic laws hold:
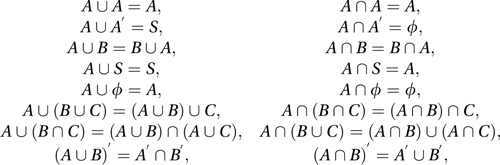 where A′ and B′ are the complementary events of A and B respectively, and φ is the empty set. The last line of the above comprises the de Morgan laws. The penultimate line comprises the distributive laws and the ante-penultimate line comprises the associative laws.
where A′ and B′ are the complementary events of A and B respectively, and φ is the empty set. The last line of the above comprises the de Morgan laws. The penultimate line comprises the distributive laws and the ante-penultimate line comprises the associative laws.
An algebra that is particularly important in computing. Formally it is a complemented distributive lattice. In a Boolean algebra there is a set of elements B that consists of only 0 and 1. Further there will be two dyadic operations, usually denoted by ∧ and ∨ (or by. and +) and called and and or respectively. There is also a monadic operation, denoted here by ′, and known as the complement operation. These operations satisfy a series of laws, given in the table, where x, y, and z denote arbitrary elements of B.
There are two very common examples of Boolean algebras. The first consists of the set
with the dyadic AND and OR operations replacing ∧ and ∨ respectively, and the NOT operation producing complements. Thus 1 and 0 are just TRUE and FALSE respectively. This idea can be readily extended to the set of all n-tupleswhere each xi is in B. The AND and OR operations are then extended to operate between corresponding pairs of elements in each n-tuple to produce another n-tuple; the NOT operation negates each item of an n-tuple.The second common example of a Boolean algebra is the set of subsets of a given set S, with the operations of intersection and union replacing ∧ and ∨ respectively; set complement fills the role of Boolean algebra complement.
Boolean algebras, named for George Boole, the 19th-century English mathematician, are fundamental to many aspects of computing—logic design, logic itself, and aspects of algorithm design. See table.

Boolean algebra. Laws
An algebra introduced by George Boole in 1854 originally to provide a symbolic method for analysing human logic. Almost a century later it was also found to provide a means for analysing logical machines. An algebra is a collection of sets together with a collection of operations over those sets. A Boolean algebra may be defined as a set K of Boolean values or constants, along with a set P of three operators AND, OR, and NOT, satisfying certain algebraic laws. The set K contains 2n elements, where n is a nonzero integer, and includes two special elements denoted 0 and 1. Thus in the simplest two-valued Boolean algebra, K = {0,1}. This is the basis for all digital logic design, from the simplest logic functions to complex microprocessors and computers. The set of all subsets of a given set (S) also forms a Boolean algebra, with AND, OR, and NOT being represented by the set operations intersection, union, and complement, respectively.
https://www.allaboutcircuits.com/textbook/digital/chpt-7/introduction-boolean-algebra/ An introduction to Boolean algebra for electronics engineers
A Boolean algebra is a system consisting of a set S and two operations, ∩ and ∪ (cap and cup), subject to the following axioms. For all sets a,b,c, that are members of S:
1 a ∩ (b ∩ c)=(a ∩ b) ∩ c. Also a ∪ (b ∪ c)=(a ∪ b) ∪ c (associativity)
2 a ∩ b=b ∩ a. Also a ∪ b=b ∪ a (commutativity)
3 a ∩ (b ∪ c)=(a ∩ b) ∪ (a ∩ c). Also a ∪ (b ∩ c)=(a ∪ b) ∩ (a ∪ c)(distributivity)
4 There belong to S two elements, 0 and 1, with the propertiesa ∪ 0=a; a ∩ 1=a (identity)
5 For each set a in S there exists a set a′ with the properties that a ∪ a′=1, a ∩ a′=0 (complementation).
http://www.allaboutcircuits.com/vol_4/chpt_7/index.html An online tutorial on Boolean algebra
- humectants
- Hume, David (1711–76)
- Hume, John (1937–2020)
- Hume-Rothery electron concentration rules
- Hume-Rothery rules
- Hume-Rothery, William
- humerus
- Hume’s fork
- Hume’s law
- Hume’s principle
- humic acid
- humic coal
- humid heat
- humidification
- humidity
- humid mid-latitude morphoclimatic zone
- humid tropical morphoclimatic zone
- humid volume
- humification
- humiliation
- humilis
- humite
- hummingbird
- hummocky cross-bedding
- hummocky moraine