Below, the trigonometric functions are defined, first where the angle is measured in degrees and secondly using radians.

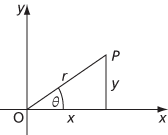
Adjacent x, opposite y, hypotenuse r.

Using degrees

The basic trigonometric functions, cosine, sine, and tangent, are first introduced by using a right-angled triangle where 0 < θ‎ < 90, but cosθ‎°, sin θ‎°, and tanθ‎° can also be defined when θ‎ is larger than 90 and when θ‎ is negative. Let P be a point (not at O) with Cartesian coordinates (x,y). Suppose that OP makes an angle of θ‎° with the positive x-axis and that |OP|=r. Then the following are the definitions:

$$\text{sin}\theta °=\frac{y}{r}=\frac{\text{opposite}}{\text{hypotenuse}},\text{cos}\theta °=\frac{x}{r}=\frac{\text{adjacent}}{\text{hypotenuse}},\text{tan}\theta °=\frac{y}{x}=\frac{\text{adjacent}}{\text{opposite}}\left(x\ne 0\right).$$

It follows that tanθ‎° = sinθ‎°/cosθ‎°, and that cos²θ‎° + sin²θ‎° = 1. Some of the most frequently required values are given in the table.

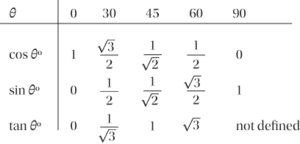
Common values

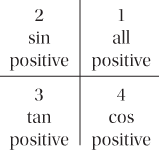
Parity by quadrant

The point P may be in any of the four quadrants. By considering the signs of x and y, the quadrants in which the different functions take positive values can be found and are shown in the figure.

The following are useful for calculating values, when P is in quadrant 2, 3, or 4:

$$\begin{array}{l}\text{cos}{(180-\theta )}^{°}=-\text{cos}{\theta }^{°},\hfill \\ \text{sin}{(180-\theta )}^{°}=\text{sin}{\theta }^{°},\hfill \\ \text{cos}{(180+\theta )}^{°}=-\text{cos}{\theta }^{°},\hfill \\ \text{sin}{(180+\theta )}^{°}=-\text{sin}{\theta }^{°},\hfill \\ \text{cos}{(-\theta )}^{°}=\text{cos}{\theta }^{°},\hfill \\ \text{sin}{(-\theta )}^{}=-\text{sin}{\theta }^{}.\hfill \end{array}$$

The functions cosine and sine are periodic, of period 360; that is to say, cos(360 + θ‎)° = cos θ‎° and sin(360 + θ‎)° = sin θ‎°. The function tangent is periodic, of period 180; that is, tan(180 + θ‎)° = tan θ‎°.

Using radians

In more advanced work, particularly involving calculus, it is essential that angles are measured in radians. The functions sine, cosine, and tangent are defined by the same trigonometric ratios but, with angles now measured in radians, sin, cos, and tan are technically different functions from when degrees are used. For example, the functions cos and sin now have period 2π‎, and tan has period π‎.

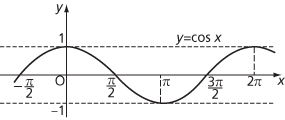
Graph of cosx

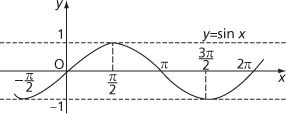
Graph of sinx

For identities connecting the trigonometric functions, see appendix 14. These identities apply whether degrees or radians are used.

The other trigonometric functions, cotangent, secant, and cosecant, are defined as follows:

$$\text{cot}x=\frac{\text{cos}x}{\text{sin}x},\text{sec}x=\frac{1}{\text{cos}x},\text{cosec}x=\frac{1}{\text{sin}x},$$

where, in each case, values of x that make the denominator zero must be excluded from the domain.

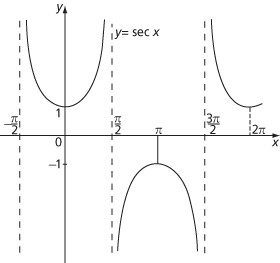
Graph of secx

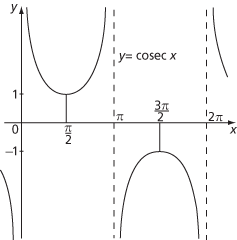
Graph of cosecx

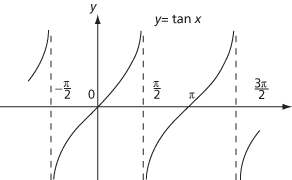
Graph of tanx

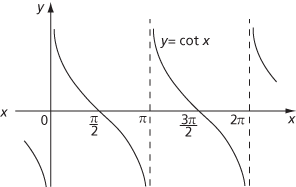
Graph of cotx

When radians are used, the derivatives of sinx and cosx are

$$\frac{\text{d}}{\text{d}x}\left(\text{sin}x\right)=\text{cos}x,\frac{\text{d}}{\text{d}x}\left(\text{cos}x\right)=-\text{sin}x.$$

The derivatives of the other trigonometric functions are found from these, by using the rules for differentiation, and are given in Appendix 7.

The complex trigonometric functions can be defined in terms of the trigonometric series expansions or in terms of the complex exponential by

$$\text{cos}z=\frac{\text{exp}\left(iz\right)+\text{exp}\left(-iz\right)}{2},\text{sin}z=\frac{\text{exp}\left(iz\right)-\text{exp}\left(-iz\right)}{2i}.$$

Euler’s formula exp(iz) = cosz + isinz then holds for all complex z, though it does not follow that cosz is the real part of exp(iz) in general. Likewise, the identity cos²z + sin²z = 1 still holds for all complex z.

The trigonometric and hyperbolic functions are then related by

$$\text{sin}\left(iz\right)=i\text{sinh }z,\text{cos}\left(iz\right)=\text{cosh }z$$

for all complex z.