A well-known, but intriguing probability problem. There are n people in a room. Assume that none is born on 29 February and that the remaining 365 days are all equally likely as birthdays. What is the smallest value of n for which the probability that at least two have the same birthday is greater than 0.5?
The answer is not 183, but 23. The complementary event is that all n people have different birthdays. The probability of this, pn, is
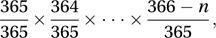which reduces surprisingly quickly as n increases:n
3
5
9
13
16
19
22
23
26
30
34
40
46
pn
0.99
0.97
0.91
0.81
0.72
0.62
0.52
0.49
0.40
0.29
0.20
0.11
0.05
- commercial policy
- commercial presence
- commercial spaces
- Commines, Philippe de (1447–1511)
- comminution
- commission
- commissioning
- Commission on Classification of Minerals
- Commission on New Minerals and Mineral Names
- Commission on New Minerals, Nomenclature, and Classification
- Commission on Ore Mineralogy
- commissure
- commit
- commitment
- commit protocol
- committed
- Committee of Presidents of Statistical Societies
- Committee of Public Safety
- Committee on Earth-Observation Satellites
- Committee on Payments and Market Infrastructure
- Committee on Space Research
- Committee on the Peaceful Uses of Outer Space
- commodification
- commodity
- commodity agreement