A series representation for a function f having continuous derivatives of all orders. The series is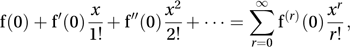where f^(r)(0) means d^rf(x)/dx^r evaluated at x=0. The series may converge for all values of x, or for |x|<R, for some positive R, or it may only converge when x=0. If f(x) is a polynomial then the series is finite and the sum is f(x). For most practical cases, if the series converges then its sum is f(x)—this is true for e^x and sin x, when the series is convergent for all x, and for (1+x)^1/2 and ln(1+x), when the series is convergent for |x|<1. In such cases the first (n+1) terms give a polynomial approximation g(x) to f(x), which has the property that at x=0, the first n derivatives of g(x) and f(x) are equal. There are however non-zero functions f such that f(x) and all its derivatives are zero at x=0, and in this case the Maclaurin series vanishes—for example, f(x)=exp (−1/x²) for x≠0, with f(0)=0.

The Maclaurin series is of use in the theoretical development of moment-generating functions and probability-generating functions. It is the particular case of a Taylor series when a=0.