Imagine three poles with a number of discs of different sizes initially all on one of the poles in decreasing order from the bottom upwards. The problem is to transfer all the discs to one of the other poles, moving the discs individually from pole to pole, so that one disc is never placed above another of smaller diameter. A version with 8 discs, known as the Tower of Hanoi, was invented by Edouard Lucas and sold as a toy in 1883, but the idea may be much older. The toy referred to a legend about the Tower of Brahma which has 64 discs being moved from pole to pole in the same way by a group of priests, the prediction being that the world will end when they have finished their task.

If t_n is the number of moves it takes to transfer n discs from one pole to another, then t_n = 2ⁿ − 1, so the original Tower of Hanoi puzzle takes 255 moves, and the Tower of Brahma takes 2⁶⁴ − 1.

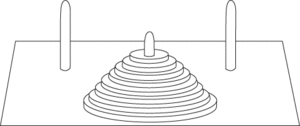
Initial position in Tower of Hanoi