A simple form of Bayes’s theorem is
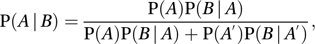 where A′ denotes the complementary event (see sample space) to the event A. For example, suppose a man has two coins in his pocket. One is unbiased, whereas the other is double headed. He takes one coin at random from his pocket and tosses it. Given that the coin falls heads, the probability that it is the double-headed coin is
where A′ denotes the complementary event (see sample space) to the event A. For example, suppose a man has two coins in his pocket. One is unbiased, whereas the other is double headed. He takes one coin at random from his pocket and tosses it. Given that the coin falls heads, the probability that it is the double-headed coin is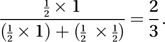 The general form is
The general form is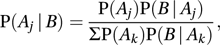 where the events A1, A2,…are mutually exclusive and exhaustive.
where the events A1, A2,…are mutually exclusive and exhaustive.
A theorem used for calculating the conditional probability of an event, where conditional probability, Prob(x|y), is the probability of x while y holds.
This is a method in probabilistic reasoning where Prob(causes|symptoms) can be computed from knowledge of Prob(symptoms|causes), i.e. if we know statistical data on the occurrence of symptoms associated with a disease we can find the probability of those symptoms correctly indicating the disease. A classic application of Bayes’s theorem is found in the Prospector expert system, which successfully predicted the location of valuable mineral deposits.
The combinatorial number of conditional probabilities that have to be computed by the method can be significantly reduced by using Bayesian networks, where arcs between propositions define causal influences and the independence of relations.
- reversal timescale
- reverse-acting controller
- reverse active operation
- reverse authentication
- reverse bias
- reverse conducting thyristor
- reversed field
- reverse direction
- reversed kink band
- reverse engineering
- reverse fault
- reverse flow plate
- reverse genetics
- reverse mathematics
- reverse osmosis
- reverse Polish notation
- reverse saturation current
- reverse slash
- reverse takeover
- reverse transcriptase
- reverse triangle inequality
- reverse video
- reverse yield gap
- reverse zoning
- reversible