If a triangle’s vertices have position vectors a,b,c, the position vector of any point of the plane containing the triangle can be written uniquely as αa + βb + γc where α + β + γ = 1. The point’s barycentric coordinates are α,β,γ. Points inside the triangle have positive barycentric coordinates. At the triangle’s centroid α=β=γ = 1/3. Barycentric coordinates can similarly be defined for a simplex.
A system of coordinates with their origin at the centre of mass of the Solar System. The reference plane is usually the ecliptic. See also Heliocentric Coordinates.
Coordinates describing the position of a point in a triangle or simplex. The position of any point P inside, or on the boundary of, a given triangle of reference A1A2A3 can be specified by finding masses m1, m2, m3 such that P is the centre of mass of particles of masses m1, m2, m3 placed at A1, A2, A3 respectively. In this case P is said to have barycentric coordinates (m1, m2, m3). For an internal point of the triangle the masses are all positive. If k>0 then (km1, km2, km3) represents the same point, so barycentric coordinates are usually chosen so that m1+m2+m3=1. With this convention, the barycentric coordinates of A1 are (1, 0, 0), and those of the midpoint of A1A2 are (, , 0). Suppose a random trial can result in one of three possibilities with probabilities p1, p2, p3, such that p1+p2+p3=1, then allocation of these probabilities can be represented by a point inside, or on the boundary of, the triangle. The triangular display is sometimes referred to as a ternary diagram. The idea of barycentric coordinates can be generalized to the case of a tetrahedron in three dimensions or a simplex. See also areal coordinates.
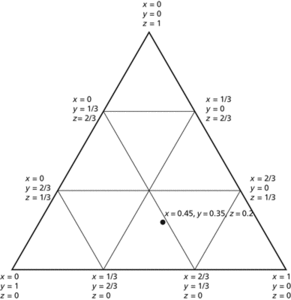
Barycentric coordinates. Illustrated for compositions of three classes having proportions x, y, and z. The case where the three classes are equally likely corresponds to the centroid of the equilateral triangle.